arigirisu2014-alphametic

覆面算 Alphametic

覆面算（ふくめんざん）は、0から9の数字がそれぞれに対応する別の記号に置き換えられた計算式を与えられ、どの記号が何の数字に対応しているかを推理し、完全な計算式を導き出すパズルです。
Alphameticは、Alphabetとarithmetic(算術)の合成語です。
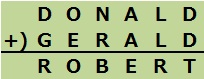
■例題１　DONALD+GERALD=ROBERT
■例題２　SEND+MORE=MONEY
■例題３　虫食い算
■例題４　虫食い算作成プログラム

例題１

○問題の解き方
使用されている文字は、D,O,N,A,L,G,E,R,B,Tの10種類。
これらの文字に0から9までの数字を割り当てる。
このとき、一度使用した数字は使わない。
○C言語ソースリスト
 ○答え
 ○ページtopに戻る
最終更新：2011年4月21日

○紙と鉛筆で解く

(1)文字間の関係式を書いてみます。a, b, c, d, eは繰り上がった数字です。題意からこれらはすべて0か1です。
2D=10a+T--------------①
2L+a=10b+R-----------②
2A+b=10c+E-----------③
N+R+c=10d+B---------④
O+E+d=10e+O---------⑤
D+G+e=R---------------⑥

(2)e=0の場合
⑤よりE+d=0。これを満たすのはE=0, d=0だけ。
よって③は、2A+b=10c。ここでc=0とすると2A+b=0となりこれを満たすのはA=0, b=0となるがすでに0は使用済。
したがってc≠0。すなわちc=1です。
よって③は、2A+b=10となる。変形してb=10-2A。すなわちbは偶数。よってb=0, A=5。

i)a=0の場合
2D=T---------------------①'
2L=R---------------------②'
N+R+1=B----------------④'
D+G=R-------------------⑥'
未使用：1,2,3,4,6,7,8,9--------⑦
②'よりRは偶数。よって⑥'よりD+Gも偶数。
さらに⑦よりD,Gの組み回せを考えると、(1,3), (1,7), (2,4), (2,6)の4通りのみ。
すると②'',④'はそれぞれ以下のようになる。
(1,3)のとき　R=4, L=2, N+5=B----これを満たすN, Bは、(2,7), (4,9)の2通り。しかし、2,4は使用済。不適
(1,7)のとき　N+9=B----B<10だからこのようなＮは存在しない。不適
(2,4)のとき　R=6, L=3, N+7=B----これを満たすN, Bは、N=1, B=8のみ
　　　(N,B)=(1,8)のとき、未定文字はO,Tで未使用は7,9。①'よりTは偶数なのに未使用に偶数なし。不適
(2,6)のとき　N+9=B----B<10だからこのようなＮは存在しない。不適
以上からa≠0。すなわちa=1である。

ii)a=1の場合
2D=10+T-----------------①''
2L+1=R-------------------②''
N+R+1=B----------------④'
D+G=R-------------------⑥'
未使用：1,2,3,4,6,7,8,9--------⑦
②''よりRは奇数。よって⑥'よりD+Gも奇数。
さらに⑦よりD,Gの組み合わせを考えると、(1,2), (1,4), (1,6), (1,8), (2,3), (2,7), (3,4), (3,6)の8通りのみ。
すると②'',④'はそれぞれ以下のようになる。
(1,2)のとき　R=3, L=1----1は使用済なので不適
(1,4)のとき　R=5, L=2----5は使用済なので不適
(1,6)のとき　N+8=B----B<10だからこれを満たすNは0,1しかないがいずれも使用済。不適
(1,8)のとき　N+10=B----B<10だからこのようなＮは存在しない。不適
(2,3)のとき　R=5, L=2----2, 5は使用済なので不適
(2,7)のとき　N+10=B----B<10だからこのようなＮは存在しない。不適
(3,4)のとき　R=7, L=3----3は使用済なので不適
(3,6)のとき　N+10=B----B<10だからこのようなＮは存在しない。不適

以上からe=0とした場合、すべて不適。よってe=1である。

(3)e=1の場合
⑤よりE+d=10。E=9, d=1だけ。
よって③は、2A+b=10c+9。ここでc=0とすると2A+b=9。2Aは偶数だからbは奇数。よってb=1, A=4となる。
一方c=1とすると2A+b=19。同様にb=1, A=9となるが、9は使用済なので不適。
以上からb=1, c=0, A=4が確定。

i)a=0の場合
2D=T---------------------①'
2L=10+R-----------------②'
N+R=10+B--------------④'
D+G+1=R-------------------⑥'
未使用：0,1,2,3,5,6,7,8--------⑦'
②'よりRは偶数。よって⑥'よりD+Gは奇数でD+G<8。
さらに⑦'よりD,Gの組み回せを考えると、(0,1), (0,3), (0,5), (0,7), (1,2), (2,3), (2,5)の7通りのみ。
すると②'',④'はそれぞれ以下のようになる。
(0,1)のとき　R=2, L=6, N=8+B----これを満たすBは存在しないので不適
(0,3)のとき　R=4, L=7, N=6+B----4は使用済みなので不適
(0,5)のとき　R=6, L=8, N=4+B----これを満たすN, Bは、(7,3)のみ。
　　(N,B)=(7,3)のとき、未定文字はO,Tで未使用は1,2。①'よりTは偶数だから T=2, D=1。しかしDは0か5だから不適
(0,7)のとき　R=8, L=9--------------9は使用済みなので不適
(1,2)のとき　R=4, L=7--------------4は使用済みなので不適
(2,3)のとき　R=6, L=8, N=4+B----これを満たすN, Bは、(5,1)のみ。
　　(N,B)=(5,1)のとき、未定文字はO,Tで未使用は0,7。①'よりTは偶数だからT=0, D=0。不適
(2,5)のとき　R=8, L=9--------------9は使用済みなので不適
以上からa≠0。すなわちa=1である。

ii)a=1の場合
2D=10+T-----------------①''
2L=9+R-------------------②''
N+R=10+B----------------④'
D+G+1=R-------------------⑥'
未使用：0,1,2,3,5,6,7,8--------⑦'
②''よりRは奇数。よって⑥'よりD+Gは偶数でD+G<7。。
さらに⑦よりD,Gの組み合わせを考えると、(0,2), (0,6), (1,3), (1,5)の4通りのみ。
すると②'',④'はそれぞれ以下のようになる。
(0,2)のとき　R=3, L=6, N=7+B----これを満たすN, Bは、(8,1)の1通り。
　　　(N,B)=(8,1)のとき、未定文字はO,Tで未使用は5,7。①''よりTは偶数だから候補なし。不適
(0,6)のとき　R=7, L=8, N=3+B----これを満たすN, Bは、(5,2)の1通り。
　　　(N,B)=(5,2)のとき、未定文字はO,Tで未使用は1,3。①''よりTは偶数だから候補なし。不適
(1,3)のとき　R=5, L=7, N=5+B----これを満たすN, Bはないので不適
(1,5)のとき　R=7, L=8, N=3+B----これを満たすN, Bは、(3,0), (6,3)の2通り。
　　　(N,B)=(3,0)のとき、未定文字はO,Tで未使用は2,6。T=2ならD=6で不適。T=6ならD=8で不適。
　　　(N,B)=(6,3)のとき、未定文字はO,Tで未使用は0,2。T=0ならD=5, O=2。T=2ならD=6で不適。

以上から
E=9, A=4, D=5, G=1, R=7, L=8, N=6, B=3, T=0, O=2
これ以外ありません。
最終更新：2011年9月28日

例題 2

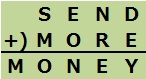この問題は、イギリスのパズル作家H. E. Dudeney(デュードニー)が発表した、世界で最も有名と思われる覆面算です。
作者/出典/参照: H. E. Dudeney / Strand Magazine 68 (1924)

○問題の解き方
使用されている文字は、S,E,N,D,M,O,R,Yの8種類。
例題1同様、これらの文字に0から9までの文字を割り当てる。
このとき、一度使用した数字は使わない。
○C言語ソースリスト
 ○答え
 ○ページtopに戻る
最終更新：2011年4月21日

○紙と鉛筆で解く
(1) まずMに着目します。Ｍは最上位桁（一番左）の文字ですから0ではありません。
また、MはS+Mを計算した結果繰り上がった数字です。
SもMも一桁の数字ですから、S+Mが20以上になることはありません。よってM=1です。

(2) 次にSに着目します。S+Mは10以上で、(1)よりM=1ですからS+1≧10。
すなわちS≧9。Sは一桁の数字ですからS=9となります。

(3)そろそろ紙と鉛筆が必要になってきました。
とにかく関係式を書いてみます。なおa,b,cは繰り上がった数字です。よってそれぞれ0か1です。

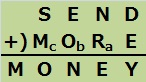D+E=10a+Y------①
N+R+a=10b+E------②
E+O+b=10c+N------③
S+M+c=10+O-------④

(1)(2)よりS=9, M=1ですからこれを④に代入すると10+c=10+O。O=cです。
cは0か1です。

c=1と仮定すると、O=1。これを③に代入するとE+1+b=10+N。
計算すると、E+b=9+N。
ここでb=1と仮定するとE=8+N。Eは一桁の数字だからNは0か1。すでに1と9は使用済なのでN=0, E=8となります。
　　　b=0と仮定するとE=9+N。Eは一桁の数字だからN=0。するとE=9となりますが、9は使用済。よって不適。

c=0と仮定すると、O=0。これを③に代入するとE+0+b=0+N。
計算すると、E+b=N。
ここでb=1と仮定するとE+1=N。
　　　b=0と仮定するとE=N。となり不適。

以上からb=1が確定しました。

(4)b=1を②に代入すると、N+R+a=10+E-------②'
ところで(3)より、NとEは、
i)N=0, E=8の場合とii)E+1=Nの場合しかないので、②'をそれぞれ確認してみます。
i)のとき②'は、
　0+R+a=10+8すなわち、R+a=18。しかしR<10ですし、aは0か1ですので、これを満たすRは存在しませんので不適。
ii)のとき②'にN=E+1を代入すると、
　E+1+R+a=10+Eすなわち、R+a=9となります。a=0とするとR=9ですが9は使用済ですので不適。よってa=1, R=8。
以上からii)が採用されますので、一気に、a=1, R=8, E+1=N, c=0, O=0が確定します。

(5)ここでまとめると、8種類の文字S,E,N,D,M,O,R,YのうちS=9, M=1, O=0, R=8の4つが確定しました。
そして、繰り上がりの数字a, b, cについても、a=1, b=1, c=0が確定しました。
さらにN=E+1という関係もわかりました。
これらをもう一度①～④に代入して整理します。
①-----D+E=10+Y
②-----E+1+8+1=10+E
③-----E+0+1=0+E+1
④-----9+1+0=10+0
要するに上の②～④は意味がありませんので、頼りは①とN=E+1の２つということになります。

改めて、
D+E=10+Y------①
N=E+1-----------⑤
未使用の数字は2,3,4,5,6,7の6個-------⑥

(6)まずDとEの組み合わせを考えてみます。
Yは⑥より2以上ですから、①より、D+Eは12以上ということになります。
⑥の中の2つ数字の組み合わせで12以上になるのは(5,7)と(6,7)しかありません。
⑤においてE=7とするとN=8となり、8は使用済なので不適。よってE≠7。
したがって、必然的にD=7となります。
未使用の数字は2,3,4,5,6の5個---------⑥'

(7)D=7を①に代入すると
7+E=10+Yすなわち、E-Y=3が得られます。
⑥'の中の2つの数字の組み合わせで差が3になるのは、(2,5),(3,6)の2通りだけです。
E>Yですから、Eは5か6です。
⑤においてE=6とするとN=7となり、7は使用済なので不適。よってE=5, Y=2。⑤よりN=6。
これで全部の数字が確定しました。
○ページtopに戻る
更新：2011年9月28日

例題3

空白文字などを使って，表すパズルもあります。日本では虫食い算と言われています。例えば，

　　□□
　×□□
　------
　　１□
　□□ 　
--------
□□□□

が成り立つように四角に数字を当てはめるといったものです。この虫食い算や Alphametic を総称して覆面算と言うこともあります。
○ページtopに戻る

○紙と鉛筆で解く
(1)まず□を文字に直します。

　　ab
　×cd
　------
　　1e
fg
--------
hijk

a,b,c,d,e,f,g,h,i,j,kは１桁の数字。題意から、a,c,f,h≠0。k=e。

(2)1+gによる繰り上がりがない場合は、h=0となり不適。
一方、1+gによる繰り上がりは高々1。よってf+1＝10h+i。
題意よりh≠0だからf+1は10以上でなければならない。よってf=9, h=1, i=0
また、1+gは繰り上がるからg=9

(3)(10a+b)d=10+e--------------①
10ad+bd=10+e
eは1桁の数字だから10+e<20
∴10ad+bd<20
よってad=0または1
ここでa≠0だから、(d=0)または(a=d=1)
一方、d=0とすると0=10+eとなり矛盾。よってd≠0
∴a=d=1
これを①に代入すると、10+b=10+e
∴b=e

(4)(10a+b)c=10f+g
これにa=1,f=9,g=9を代入すると、
(10+b)c=99---------------------------②
計算すると、
10c+bc=99
この式から、bcの1桁目は9でありことがわかる。
2つの数字をかけて1桁目が9になる組み合わせは、(b,c)=(1,9),(3,3),(7,7),(9,1)
これを②に代入してみる
　　(1,9)のとき②左辺＝11×9=99
　　(3,3)のとき②左辺＝13×3=39
(7,7)のとき②左辺＝17×7=119
(9,1)のとき②左辺＝19×1=19
以上よりb=1, c=9

よって答えは下記の１通り。

　　11
　×91
　------
　　11
　 99 　
--------
1001

○ページtopに戻る
更新：2012年9月14日

例題4

右のような虫食算の20個の＊のうち、5個は同じ数字Nです。
残り15個はNでない任意の数字です。
このような虫食算の中で、解があるものを、その解と共に全部列挙して下さい。

※この問題は「続ナノピコ教室」駒木悠二＋有澤誠編1991年3月15日、共立出版p39の内容を少し直したものです。
※問題の解き方は、arigirisuオリジナルです。
○ページtopに戻る

　　＊＊＊
×）＊＊＊
　＊＊＊
　＊＊＊
＊＊＊　　
＊＊＊＊＊

プログラムで解く

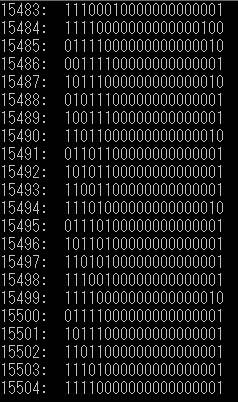
20個の＊から5か所を選ぶ組み合わせは、(20×19×18×17×16)/(5×4×3×2×1)＝15,504。
Nは0～9のどれかなので10通りあります。よって、確認すべき問題は15,504×10=155,040
紙と鉛筆では太刀打ちできませんので、アルゴリズムを考えてプログラムを作ってパソコンで解くことになります。

■方針
N=0のとき
＜列挙＞15,504個の問題が自動的に出てくるようにする
＜条件＞自動的に出てきた問題を計算して条件が成立するか確認する
＜表示＞条件が成立した問題と解を表示（印刷）する
以上をN=9まで繰り返す。

■列挙(→組み合わせ列挙プログラムの説明）

#include <stdio.h>
int num = 0;
void combi(int A[], int p, int w, int n, int r)
{
　if(p > 0)
　{
　　int i;
　　for(i = 0;i <= w;i++)
　　{
　　　A[p] = i;
　　　combi(A, p - 1, w - i, n, r);
　　}
　} else {
　　int i, j, m;
　　num++;
　　printf("%d:\t", num);
　　m = 0;
　　for(i = 1;i <= r;i++){
　　　for(j = 0;j < A[i];j++, m++)
　　　printf("0");
　　　printf("1");
　　　m++;
　　}
　　for(;m < n;m++)
　　printf("0");
　　printf("\n");
　}
}

int main(void)
{
　int n = 20;
　int r = 5;
　int K[16000];
　combi(K, r, n-r, n, r);
　return 0;
}

top＞
○ページtopに戻る
最終更新：2012年10月16日