ガロア理論 Galois theory

エバリスト・ガロア(Evariste Galois)は、1811年10月25日、フランス、パリの南にあるブール・ラ・レーヌという小さな村に生まれた。フランス革命から22年後のことである。当時ナポレオン・ボナパルトは権力の絶頂期にあったが、翌年にはロシア遠征で壊滅的な敗北を喫し、1814年には流刑となってルイ18世にその座を開け渡すことになった。1815年、ナポレオンはエルバ島を脱出してパリに舞い戻り、再度権力の座についたが、わずか100日にしてワーテルローの戦いに敗れ、再びルイ18世によって帝位を退かされる。ガロアは、この激動の時代に成長した。
ガロアはしばしば政治紛争の真っただ中にあり、そのことが、ガロアに数学者としての輝かしい人生から足を踏み外させたばかりか、早すぎる死へと彼を追いやることになった。(「フェルマーの最終定理」 サイモン・シンより)
※このページは、
「天才ガロアの発想力 対照性と群が明かす方程式の秘密」小島 寛之、技術評論社、2010年9月25日
「ガロアの群論」中村 亭、講談社 BLUE BACKS、2010年5月20日
「ガロワと方程式」草場 公邦、朝倉書店、1989年7月10日
「数学ガール ガロア理論」結城 浩、ソフトバンク クリエイティブ、2012年5月
「ガロア理論講義[増補版]」足立 恒雄、日本評論社、2010年7月1日増補版第2刷
「数学のかんどころ14 ガロア理論(Galois Theory)」木村 俊一、共立出版、2013年6月10日初版2刷
を参考にしています。
ガロア略年表
| 年齢 | 西暦 | |
| 0 | 1811年10月 | 25日、エヴァリスト・ガロア誕生 |
| 11 | 1823年10月 | リセ(高等中学校)「ルイ・ル・グラン」入学 |
| 15 | 1827年 1月 | 留年、数学と出会う |
| 16 | 1828年 8月 | 第1回のエコール・ポリテクニク入試(不合格) |
| 1828年10月 | 教師リシャールと出会う | |
| 17 | 1829年 5月 | 科学アカデミーに論文を提出。コーシーから、数学論文大賞へ応募し直すように勧められる。 |
| 1829年 7月 | ガロアの父が自殺。第2回のエコール・ポリテクニク入試(不合格)エコール・ポリテクニクの受験資格を失う | |
| 1829年 8月 | 進路に悩んだ後、エコール・プレパラトワール入試(合格) | |
| 18 | 1830年 2月 | 科学アカデミー数学論文大賞に論文を提出(この論文は査読者フーリエの死去のために紛失) |
| 19 | 1831年 1月 | 新聞への投書をきっかけに、共和主義活動のため放校処分。 科学アカデミーに論文を提出。7月に、査読者ポアソンとラクロアはこの論文を却下。 (この論文が現存する第一論文である) |
| 1831年 5月 | 乾杯事件のため逮捕され、刑務所へ入所 | |
| 1831年 6月 | 無罪判決 | |
| 1831年 7月 | ポン・ヌフ橋を渡るところで再逮捕され、刑務所へ入所 | |
| 20 | 1831年12月 | 有罪判決(1832年4月29日まで服役) |
| 1832年 3月 | コレラの流行に伴い、刑務所から療養所へ移送。医師の娘ステファニーと出会う。 | |
| 1832年 5月 | 29日、親友シュヴァリエへの最後の手紙、第一論文の推敲 | |
| 30日、決闘 | ||
| 31日、病院で死去 |
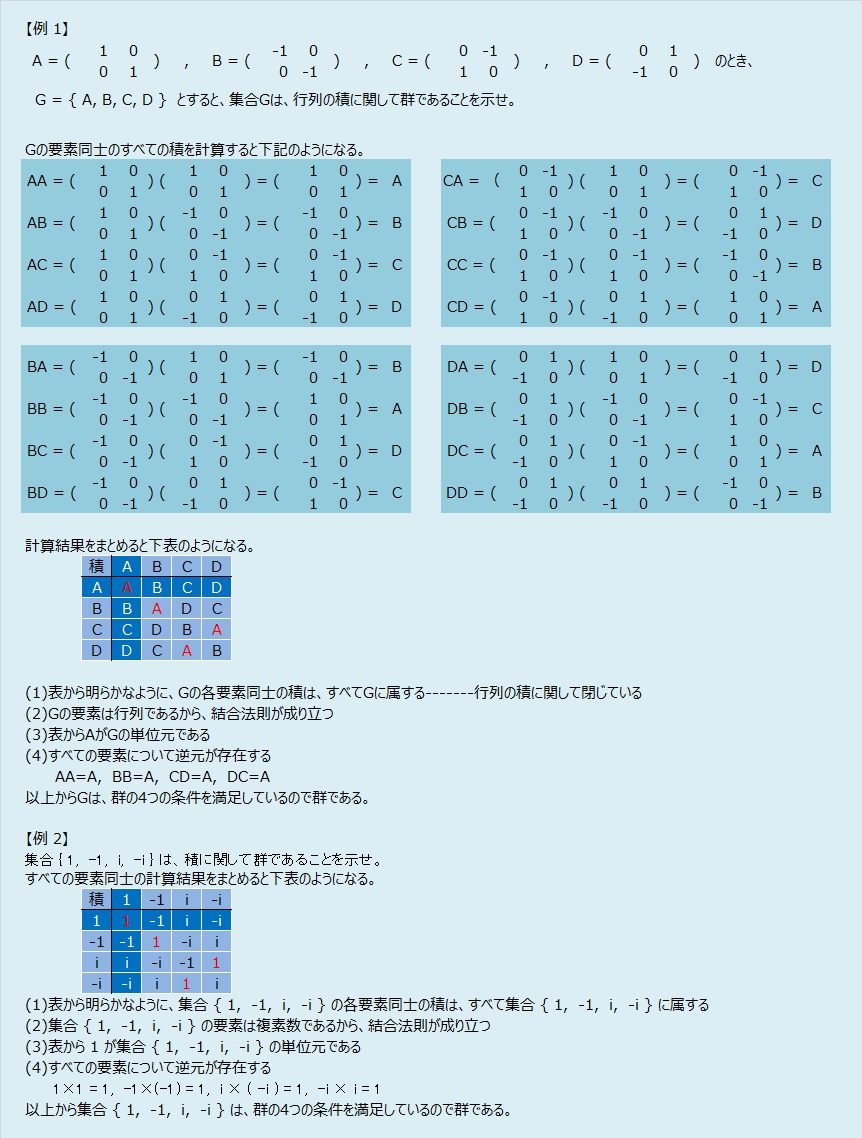
群(ぐん)の定義
集合G が次の条件を満足するとき、G は群であるといい、e をGの単位元、f-1を f の逆元という。
(1) f∈G、g∈Gのとき、g#fが定義され、g#f∈G------------演算#に関して閉じている
(2) f∈G、g∈G、h∈Gのとき、h#(g#f) = (h#g)#f--------結合法則が成立する
(3) f∈Gのとき、f#e = e#f = f である要素eがGの中にある-----単位元が存在する
(4) f∈Gのとき、f#f-1 = f-1#f = e となる要素f-1がGの中にある-----逆元が存在する
第一論文
ガロアの第一論文は、「方程式が代数的に解けるための必要十分条件」を【原理】と【応用】で論じている。
ここでは【原理】の部分を確認する。1831年当時「群」・「体」の用語がなく、ガロアは「群」・「体」という言葉は使わなかったが、ここでは「群」・「体」という用語を使って説明する。
概要
第一論文は、
・定義(可約と既約)
・定義(置換群)
・補題1(既約多項式の性質)→補題2(根でつくるV)→補題3(Vで根を表す)→補題4(Vの共役)
・定理1(「方程式のガロア群」の定義)
・定理2(「方程式のガロア群」の縮小)
・定理3(補助方程式のすべての根を添加)
・定理4(縮小したガロア群の性質)
・定理5(方程式が代数的に解ける必要十分条件)
というストーリーで進みます。
定義(可約と既約)
| 【可約と既約】 f(x)を、体Kを係数体とするxの多項式とする。 多項式f(x)が体Kで因数分解できるとき、K上で可約であるという。 可約でないとき、f(x)はK上で既約であるという。 |
ガロアは、有理数体Qを考えたり、有機数体に係数を添加した体Q(a,b)、さらに冪根などの数を添加した体Q(a,b,√2,?2)を考えたりして、それぞれの体が可約か既約か議論しようとしています。
定義(置換群)
| 【置換群】 置換を一つの群として考えるときは、ある一つの順列から始まるものとする。最初の順列に依らない問題だけを扱うのので、群に置換S, Tが属しているなら、置換STもその群に属している。 |
補題1(既約多項式の性質)
| 【既約多項式の性質】 f(x)を体K上の多項式とし、p(x)を体K上の既約多項式とする。 f(x)とp(x)が共通の根を持つならば、f(x)はp(x)で割り切れる。 |
※話はかわるが、整数に関する下記の命題を考えると、「多項式」と「整数」はよく似ていることがわかります。
それで、多項式は「整式」とも呼ばれます。
| Nを整数とし、Pを素数とする。 NとPが共通の素因数を持つならば、NはPで割り切れる。 |
| 多項式の世界 | ←→ | 整数の世界 | |
| 多項式 | ←→ | 整数 | |
| 既約多項式 | ←→ | 素数 | |
| 可約多項式 | ←→ | 合成数 | |
| 共通の根を持つ | ←→ | 共通の素因数を持つ |
f(x)=x4-1を有理数体Q上の多項式とし、p(x)=x2+1を有理数体Q上の既約多項式とする。
→有理数体Q上の多項式とは、係数がQという有理数体に属している多項式ということです。
(簡単にいうと係数が有理数であるということ)
→p(x)=x2+1について
多項式の因数分解ができるかできないかを議論するとき、どの体で考えるかを明確にする必要がありました。
多項式x2+1は有理数体の範囲で考えるなら因数分解できませんから既約多項式ですが、複素数体の範囲で考えるな らx2+1=(x+i)(x-i)のように因数分解できるので可約多項式になります。
このとき、f(x)とp(x)は共通の根をもつでしょうか?
f(i)=i4-1=0
p(i)=i2-1=0
よって共通の解iをもつ。
→f(x)やp(x)は有理数体Q上の多項式ですので、係数は有理数体に属していないといけませんが、解は有理数体に属し ていなくとも良い。
f(x)とp(x)が共通の解を持ちました。f(x)はp(x)で割り切れるでしょうか?
f(x)=(x2+1)(x2-1)
=(x2+1)(x+1)(x-1)
=p(x)(x+1)(x-1)
よってf(x)はp(x)で割り切れる。
補題2(根で作るV)
| 【根で作るV】 f(x)を重根を持たないK上の多項式とし、f(x)の根をα1,α2,α3,…,αmとする。 このとき、 根の有理式Vで、根の順序を変えると値が変わるものが構成できる。 ここで、このVを次のように表すことにする。 V=φ(α1,α2,α3,…,αm) ただし、φ(α1,α2,α3,…,αm)は、K上の有理関数とする。 さらに、この有理関数は、 整数係数(k1,k2,k3,…,km)の線形結合で書ける。 φ(x1,x2,x3,…,xm)=k1x1+k2x2+k3x3+…+kmxm |
m=2の例で考えます。
f(x)=x2+1とします。よってα1=i, α2=-i。
このとき、
根の有理式Vで、根の順序を変えると値が変わるものを構成できるかどうか?
たとえばV=α1-α2はどうでしょうか?
①α1=i, α2=-iのときは、V=i-(-i)=2i
②α1=-i, α2=iのときは、V=-i-i=-2i
たしかにVの値は変わりました。
【例2】
m=3の例で考えます。
f(x)=(x2+1)(x-1)とします。よってα1=i, α2=-i, α3=1。
このとき、
根の有理式Vで、根の順序を変えると値が変わるものを構成できるかどうか?
たとえばV=α1-α2 -α3 はどうでしょうか?
①α1=i, α2=-i, α3=1のときは、V=i-(-i)-1=2i-1
②α1=1, α2=i, α3=-iのときは、V=1-i-(-i)=-2i+1
たしかにVの値は変わりました。
補題3(Vで根を表す)
| 【Vで根を表す】 補題2のVで、f(x)の根α1,α2,α3,…,αmを表せる。すなわち、 α1=φ1(V), α2=φ2(V), α3=φ3(V),…, αm=φm(V) を満たすK上の有理関数φ1(V), φ2(V), φ3(V),…, φm(V)が存在する。 |
f(x)=x2+1、α1=i, α2=-iで、V=α1-α2でした。
このVで、α1, α2を表せるかどうか?
α1=i, α2=-iより、V=i-(-i)=2i
∴α1=V/2, α2=-V/2
たしかに、2つの根はVで表せました。
【例2】補題2の例2のVで確認します。
f(x)=(x2+1)(x-1)、α1=i, α2=-i, α3=1で、V=α1-α2 -α3 でした。
このVでα1, α2, α3を表せるかどうか?
α1=i, α2=-i, α3=1より、V=i-(-i)-1=2i-1→2i=V+1→∴i=(V+1)/2
∴α1=i=(V+1)/2
∴α2=-i,=-(V+1)/2
∴α3=1=-i2=-[(V+1)/2]2=-(V+1)2/4
たしかに、3つの根はVで表せました。
補題4(Vの共役)
| Vを根とするような、体K上の最少多項式fv(x)を新たに作り、fv(x)の根をV1, V2, V3,…, Vmとする。 このとき、 φ1(Vk), φ2(Vk), φ3(Vk), …, φm(Vk) は多項式f(x)の根の順列になる(k=1,2,3,…,n)。 |