ハノイの塔 Tower of Hanoi
ハノイの塔と呼ばれるパズルがあります。3本の棒があり、その1本にN枚の円盤がはめてあります。円盤は上から下へと順次大きくなっています。問題はこのN枚の円盤をそっくり別の棒に移動することです。ただし、円盤を移動する際、次の制限があります。
・一度に一枚の円盤を現在の棒から別の棒へ移す。
・小さい円盤の上に大きな円盤を載せてはいけない。
円盤の移動法を指示するプログラムを作りなさい。
この問題も、私が大学生時代(1984年)の授業の課題で出されたものの一つです。再帰呼び出しに関する授業の直後に出されたので、比較的簡単にクリアできたと記憶しています。
※このページは、「再帰の技法」 基本的考え方・アルゴリズム・プログラミング(2006年11月10日 玉井 浩、エスアイビー・アクセス)を参考にしています。
考え方
問題をはっきりさせるために、3本の棒にA, B, Cと名前を付けます。また円盤には円盤1から円盤Nと番号を付けます。そして最初AにはめてあるN枚の円盤を、Bを補助に使って、最終的にCに移すものとします。
「①AにはめてあるN枚の円盤をBを補助に使ってCに移す」という命題です。
もちろん、途中でむだな移動はしないものとします。
まず、一番下にある一番大きな円盤に注目しましょう。全体をCに移動するためには、この一番大きな円盤をCに移動しなければなりません。一度に一枚の円盤しか動かせないので、この円盤をCに動かすためにはその上にあるN-1枚の円盤をそっくりBに移動しておく必要があります。
「②AにはめてあるN-1枚の円盤をCを補助に使ってBに移す」という移動先の棒が違うだけの規模の小さな命題が登場しました。これすなわち再帰です。
続いて①を実現するためには、②の後、「③Aにはめてある一番大きな円盤をCに移し」、「④BにはめてあるN-1枚の円盤をAを補助に使ってCに移して」終了になります。
④は移動元の棒が違うだけの同様な命題です。もちろん再帰です。
つまり、ハノイの塔のプログラムは、再帰部分が2つ(②と④)含む構造であることがわかります。
手続きhanoi(n, x, y, z)
棒xにはめてあるn枚の円盤を棒yを補助に使って棒zへ移動する手続きをhanoi(n, x, y, z)と定義します。
すると、①②④は次のようにあらわすことができます。
①hanoi(N, A, B, C)
②hanoi(N-1, A, C, B)
③円盤NをAからCに移動する
④hanoi(N-1, B, A, C)
なお、N=1のときは③を行って終了です。
手続きhanoi(n, x, y, z)のプログラムは次のようになります。

ポイントは、引数に補助になる棒も加えることによって、①②④における移動元、補助、移動先の関係が不変であるということです。
解答プログラム
ついでですので、何手で移動が完了するかカウントするにはどうしましょうか?手数は、printfが実行される回数と同じですので、カウンタをprintfのところで1つずつ増やしていけばよさそうです。
さらに、main関数のところでNをいくつにするか決めると、最終的なプログラムは下記のようになります。
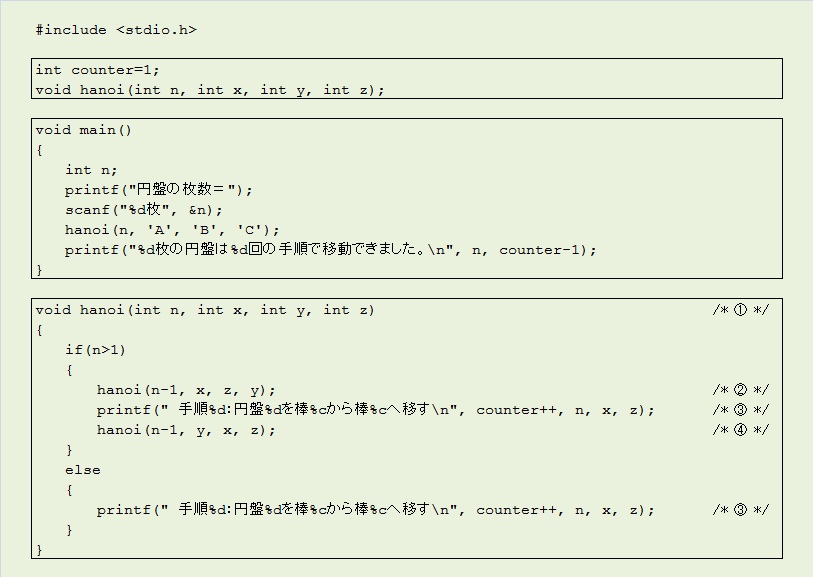
実行結果(N=3のとき)は以下の通りです。
円盤の数Nと手順数の関係
円盤の数Nと手順数の関係はどうなっているでしょうか?
| N | 手順数 | |
| 1 | 1 | 21-1 |
| 2 | 3 | 22-1 |
| 3 | 7 | 23-1 |
| 4 | 15 | 24-1 |
| 5 | 31 | 25-1 |
| 6 | 63 | 26-1 |
| 7 | 127 | 27-1 |
| 8 | 255 | 28-1 |
| 9 | 511 | 29-1 |
| ... | ... | ... |
| n | 2n-1 |
表をみると、円盤の数がnのときの手順数は 2n-1と推定できます。
この証明は以下の通りです。
2n-1の証明
円盤n枚のときの手順数をP(n)とします。
手続きhanoiの構造より、P(n)は、②P(n-1)と③P(1)と④P(n-1)の和。
P(1)=1なので、
P(n)=P(n-1)+1+P(n-1)
=2P(n-1)+1
という漸化式が得られます。
両辺に1を加えて
P(n)+1=2P(n-1)+2
=2{P(n-1)+1}
ここでQ(n)=P(n)+1とおくと
Q(n)=2Q(n-1)
すなわち、Q(n)は公差2の等比数列といえます。よって、
Q(n)=初項×公差n-1
初項=Q(1)=P(1)+1=2, 公差=2ですから、
Q(n)=2×2n-1=2n
∴P(n)=Q(n)-1=2n-1 <証明終わり>
| インドのベナレスの寺院に3本のダイヤモンドの杭があり、その1本に64枚の金の円盤がはめてあって、それを僧侶が別の杭にせっせと移している。移し終わる前に寺院は塵芥(じんかい)と化し、雷鳴と共に世界は破滅するであろう。 |
というようなことが書かれていたそうです。ベナレスがハノイに変わっていますが、それはともかく、この話はN=64とし、1枚の金の円盤を移動するのに1秒かかるとして、全部移動し終えるのにどれぐらい時間が掛かるのか計算すると、説明書の意味が理解できます。
すなわち、264-1秒≒264≒1.84467×1019秒
1年を秒に直すと、3600(秒/時間)×24(時間/日)×365(日)=31,536,000(秒)=3.1536×107(秒)ですので、
264秒は、1.84467×1019÷(3.1536×107)=5.8494×1011年≒5850億年。
余談ですが、ビックバンは今から130億年前だそうです。要するに5,850億年というのは、とても待っていられません。
この問題は補助になる棒が1本しかないから時間がかかるのです。arigirisu的には、補助の棒を63本に増やすことをお勧めします。そうすれば円盤1~63までは2回の移動、円盤64は1回の移動で目的の棒にたどりつけますので、わずか127秒で完了です。5,850億年待つぐらいなら、毎日1本の補助棒を作れば63日と127秒で解決します。
最終更新:2011年7月5日