第2ブロックについての考察
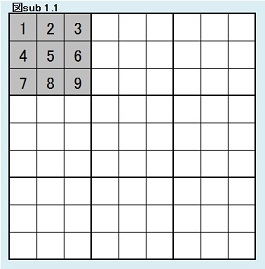 |
図sub 1.1のように第1ブロックの数字を固定したときの解総数をAとすると、N0=9!Aであることはわかった。 |
|
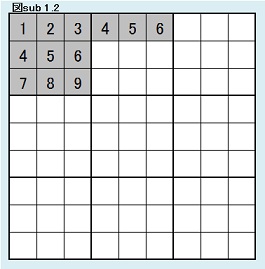 |
戸神 星也氏の論文から離れて、図sub 1.2のように第1ブロックの固定に加えて第2ブロック1行目を固定した場合どうなるか考察する。 まず、第2ブロック第1行目に入りうる数字の組み合わせは、6×5×4通りである。(6×5×4=120) 同型変換の考えよりこれら120パターンは同じ解数をもつ。 よって図sub 1.2のように第2ブロック第1行目固定の場合の解総数をBとすると、A=120Bであることがわかる。 |
|
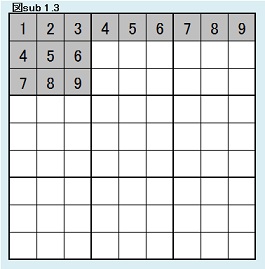 |
図sub 1.2のように固定した状態で、第3ブロック1行目を固定した場合どうなるか考察する。 同様に、第3ブロック第1行目に入りうる数字の組み合わせは、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.3のように第3ブロック第1行目固定の場合の解総数をCとすると、B=6Cであることがわかる。 |
|
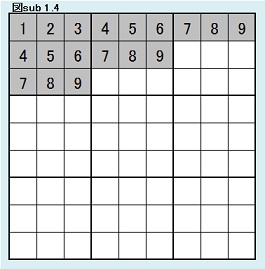 |
さて、図sub 1.3のように固定した場合の解総数Cがわかったところで、第2ブロックに戻り、第2ブロック第2行目について考察する。 ここには、7,8,9の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.4のように第2ブロック第2行目固定の場合の解総数をDとすると、C=6Dであることがわかる。 |
|
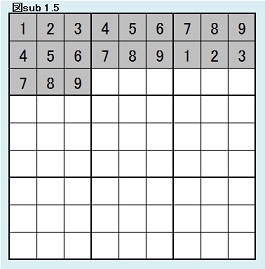 |
同様にして、第3ブロック第2行目について考察する。 ここには、1,2,3の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.5のように第3ブロック第2行目固定の場合の解総数をEとすると、D=6Eであることがわかる。 |
|
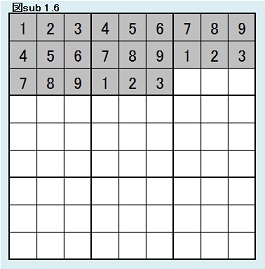 |
同様にして、第2ブロック第3行目について考察する。 ここには、1,2,3の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.6のように第3ブロック第2行目固定の場合の解総数をFとすると、E=6Fであることがわかる。 |
|
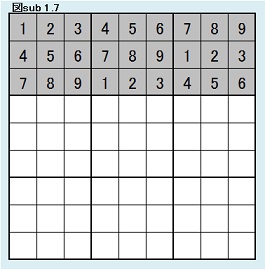 |
同様にして、第3ブロック第3行目について考察する。 ここには、4,5,6の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.7のように第3ブロック第3行目固定の場合の解総数をGとすると、F=6Gであることがわかる。 以上から、N0=9!×A =9!×120B =9!×120×6C =9!×120×6×6D =9!×120×6×6×6E =9!×120×6×6×6×6F =9!×120×6×6×6×6×6G =9!×933,120G |
|
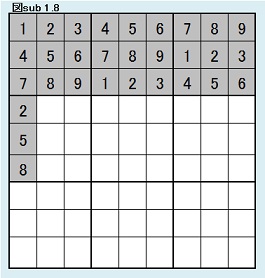 |
次に、第4ブロック第1列目について考察する。 ここには、1,4,7以外の数字が入れるので、6×5×4通りである。 (6×5×4=120) 同型変換の考えによりこれら120パターンは同じ解数をもつ。 よって図sub 1.8のように第4ブロック第1列目固定の場合の解総数をHとすると、G=120Hであることがわかる。 |
|
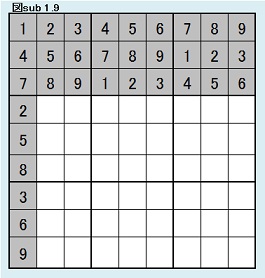 |
同様にして、第7ブロック第1列目について考察する。 ここには、3,6,9の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.9のように第7ブロック第1列目固定の場合の解総数をIとすると、H=6Iであることがわかる。 |
|
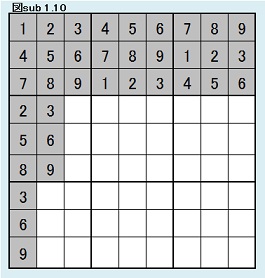 |
同様にして、第4ブロック第2列目について考察する。 ここには、3,6,9の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.10のように第4ブロック第2列目固定の場合の解総数をJとすると、I=6Jであることがわかる。 |
|
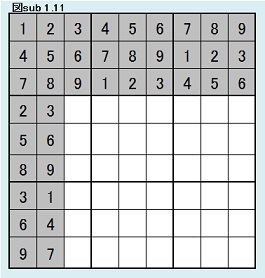 |
同様にして、第7ブロック第2列目について考察する。 ここには、1,4,7の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.11のように第7ブロック第2列目固定の場合の解総数をKとすると、J=6Kであることがわかる。 |
|
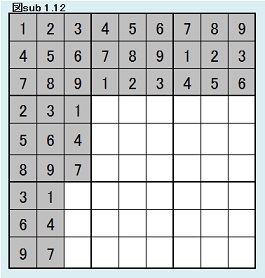 |
同様にして、第4ブロック第3列目について考察する。 ここには、1,4,7の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.12のように第4ブロック第3列目固定の場合の解総数をLとすると、K=6Lであることがわかる。 |
|
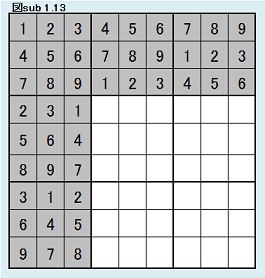 |
同様にして、第7ブロック第3列目について考察する。 ここには、2,5,8の3つの数字しか入れないから、3×2×1通りである。(3×2×1=6) 同型変換の考えによりこれら6パターンは同じ解数をもつ。 よって図sub 1.13のように第7ブロック第3列目固定の場合の解総数をMとすると、L=6Mであることがわかる。 以上から、N0=9!×933,120G =9!×933,120×120H =9!×933,120×120×6I =9!×933,120×120×6×6J =9!×933,120×120×6×6×6K =9!×933,120×120×6×6×6×6L =9!×933,120×120×6×6×6×6×6M =9!×933,120×933,120M |
第5ブロックについての考察
さて、ここまで同型変換の考え方を信じて図sub 1.13まで考察を進めてきた。
とにかく、図sub 1.13のように第1,2,3,4,7ブロックを固定た場合の解総数Mの計算だけを考えればいい。
さて、第5ブロック左上(a44)に入る候補は、5,6,8,9の4通りあるが、このことはどう考えたらいいか?
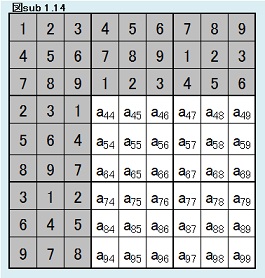
同型変換の考えにより、この4パターンも同じ解数をもつといえるか?
そこで、次に第5ブロック1行2列目(a45)に入る候補はどうなるか考えてみる。
4,6,7,9の4通りあるが、a44で何を使ったかに左右される。
a44:5のとき------a45候補4,6,7,9
a44:6のとき------a45候補4,7,9
a44:8のとき------a45候補4,6,7,9
a44:9のとき------a45候補4,6,7
以上のように、候補数が異なる。ということは、解数も違ってくると思われる。
そこで、a44~a99までに入りうる数字をまず列挙してみると下記の様になります。
(第1,2,3,4,7ブロックで使用された数字を除いた)
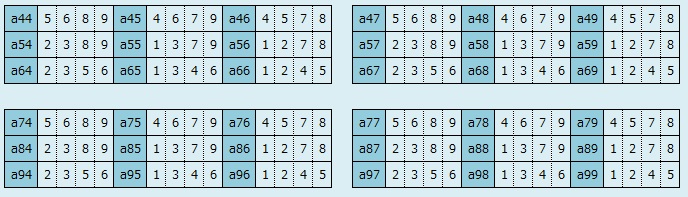
これを基に、第5ブロックで起こりうる数字の組み合わせを列挙してみます。
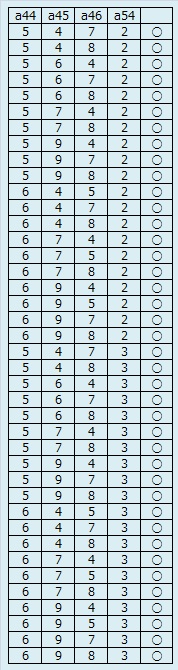
まずa44,a45,a46の64通りを列挙し、数字が重複したら×印、重複がなかったら○印をつけたのが下表左です。
×印を除くと下表中央になります。
さらにa54を追加すると下表右になります。

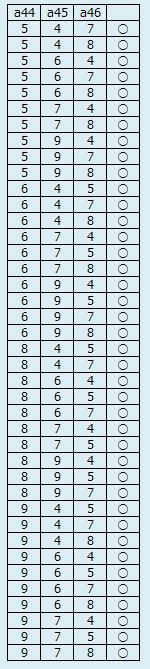
→topに戻る →ナンプレtopに戻る
開始:2013年6月14日
更新:2013年6月17日
更新:2013年6月24日
更新:2014年8月6日