確率 Probability
このページでは、信頼性試験データや初期流動データの平均値と標準偏差から量産工程の不良率を計算する方法法について考えます。目次
■正規分布■標準正規分布
■正規分布から標準正規分布への変換
■課題1.不良率の推定
■課題2.不良率の推定
正規分布 Normal Distribution →目次に戻る →topに戻る
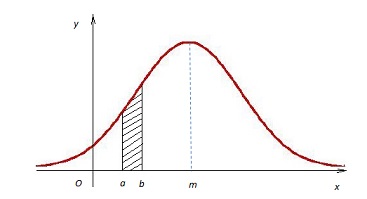 |
安定した工程で作られたもののデータの分布の姿は、左右対称の釣鐘形になることが知られています。 この形を関数で表すと下のようになります。 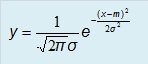 ※π:円周率、e:自然対数の底、m:平均値、σ:標準偏差 |
| 一般に、上の形の式で与えられる分布を正規分布といい、そのグラフを正規分布曲線といいます。 このようにm:平均値、σ:標準偏差が決まると正規分布が定まりますので、このような正規分布をN(m,σ2)で表します。 この正規分布曲線は、直線x=mに関して対称で、xの値がmに近いほどyの値は大きく、|x|が大きくなるとyの値は限りなく0に近づきます。 また、y=f(x)とおくと、上図の斜線で示した部分の面積 は、変量xがa<x<bの範囲にある確率P(a<x<b)です。 特に曲線とx軸との間の部分の面積は、確率P(-∞<x<∞)ですので、1です。 |
|
標準正規分布 Standard Normal Distribution →目次に戻る →topに戻る
正規分布のうち平均値m=0、標準偏差σ=1のものを特に標準正規分布と呼び、N(0,1)で表します。正規分布から標準正規分布への変換 →目次に戻る →topに戻る

課題1.不良率の推定 →目次に戻る →topに戻る
課題2.不良率の推定 →目次に戻る →topに戻る
耐熱クリープ試験を実施したところONタイミング分布:平均8.688から平均8.628に変化した。
変動分布は平均0.060であった。また、分布のバラツキ(標準偏差)は下表の通り。
| 条件 | ONタイミング | 変動分布 | ||
| 平均(m1) | 標準偏差(σ1) | 平均(m2) | 標準偏差(σ2) | |
| 初期 | 8.688 | 0.058 | ||
| 55℃3h | 0.060 | 0.034 | ||
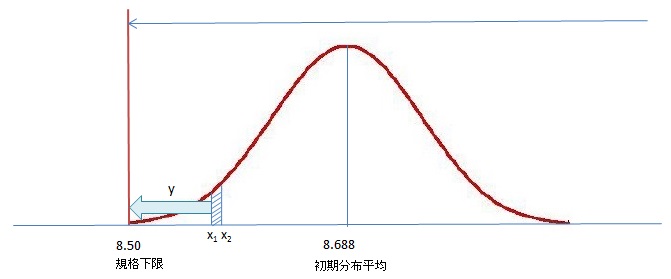
ONタイミング規格の下限が8.50のとき、耐熱クリープ試験(55℃3h)後、規格外れが発生する確率を求めよ。
 |
|
| 課題を図にすると、上のようになります。 初期分布m1=8.688, σ1=0.058のものに熱を加えたら、分布が左側に移動。 移動量は変動分布m2=0.060, σ2=0.034で与えられています。 求めるものは、移動によって規格下限8.50を下回る確率です。 |
|
| <考え方> 試験前、区間[x1,x2]に存在する確率をP(x1)とします。 区間[x1,x2]から規格下限までの距離をy1とします。 区間[x1,x2]に存在していたものがy1以上移動する確率をP(y1)とします。 求める確率は、ΣP(xn)P(yn)。 |
|
開始:2013年5月23日
最終更新:2013年5月31日