パターン別の解計算
パターンA
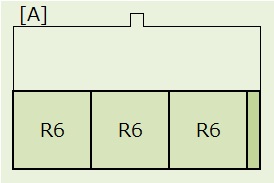R6,R6,R6,R1の順列で、4!=24通り。R6(正方形)は8通りの置き方があるので、
24×8×8×8=12,288通り
パターンB
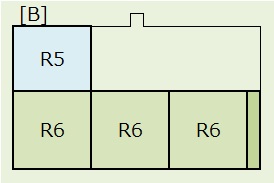
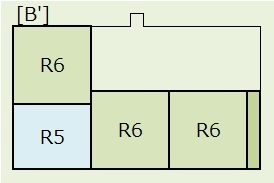
パターンBは、上図のように[B]と[B']に分けて計算します。
これは、R1を置くことができる場所が異なるからです。
1)[B]:R6,R6,R6,R1の順列で、4!=24通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 24×8×8×8×4=49,152通り。
2)[B']:R1の場所は中央R6の左側、右側、及び右R6の右側の3通り。この3通りに対して、R6,R6,R6の順列で、 3×3!=18通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、18×8×8×8×4=36,864通り。
1)2)トータルで、49,152+36,864=86,016通り
パターンC
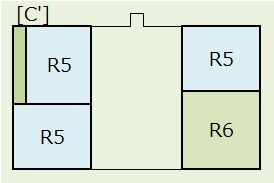
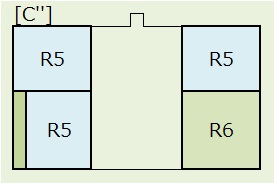
パターンCは、上図のように[C],[C'],[C'']の3つに分けて考えます。
これは、R1の場所、方向による違いです。
1)[C]:R1の場所は、上、中央、下の3通り。この3通りに対して、R5,R5,R5の順列で、3×3!=18通り。右側R5,R6交換で2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 18×2×4×4×4×8=18,432通り。
2)[C']:R1の場所は2通り。この2通りに対して、R5,R5,R5の順列で、2×3!=12通り。右側R5,R6交換で2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 12×2×4×4×4×8=12,288通り。
3)[C'']:2)同様に、12×2×4×4×4×8=12,288通り。
1)2)3)トータルで、18,432+12,288+12,288=43,008通り
パターンD
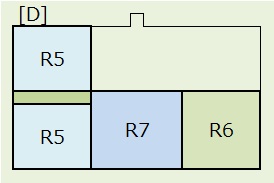
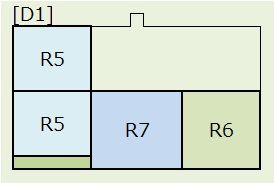
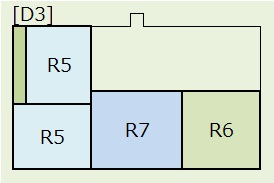
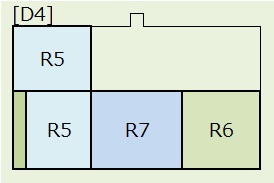
パターンDは、上図のように[D],[D1],[D2],[D3],[D4],[D5]の6つに分けて考えます。
これは、R1の場所、方向による違いです。
1)[D]:下段(R1,R5),R7,R6の順列で、3!=6通り。2つのR5は交換可能なので2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 6×2×4×4×4×8=6,144通り。
2)[D1]:下段(R5,R1),R7,R6の順列で、3!=6通り。2つのR5は交換可能なので2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 6×2×4×4×4×8=6,144通り。
3)[D2]:R7とR6の順列で、2!=2通り。2つのR5は交換可能なので2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 2×2×4×4×4×8=2,048通り。
4)[D3]:上段R1,R5の順列で、2!=2通り。2つのR5は交換可能なので2通り。R7とR6の順列で、2!=2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 2×2×2×4×4×4×8=4,096通り。
5)[D4]:下段R1,R5,R7,R6の順列で、4!=24通り。2つのR5は交換可能なので2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 24×2×4×4×4×8=24,576通り。
6)[D5]:R7,R1,R6の順列で、3!=6通り。2つのR5は交換可能なので2通り。
R6(正方形)は8通り、R5(長方形)は4通りの置き方があるので、 6×2×4×4×4×8=6,144通り。
1)～6)トータルで、6,144+6,144+2,048+4,096+24,576+6,144=49,152通り
パターンE
→topに戻る →箱詰めパズルtopに戻る →ヘキソミノtopに戻る
更新：2014年6月9日
最終更新：2014年6月10日