ヘキソミノ Gallary【C】
 |
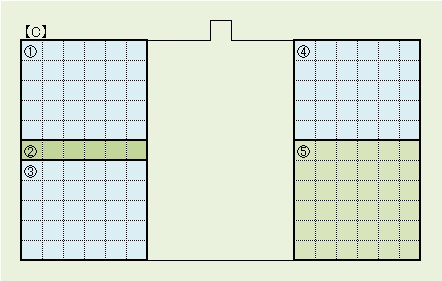②の方向、位置によって場合分けする。（→詳細） 合計84通り。 長方形は4通り、正方形⑤は8通りの置き方があるので、 84×4×4×4×8=43,008通り。 パターン【C】に収まるような入れ方を一つ発見すれば、43,008通り発見したのと同じということです。 |
当時発見した日付を記録していなかったので、通し番号です。
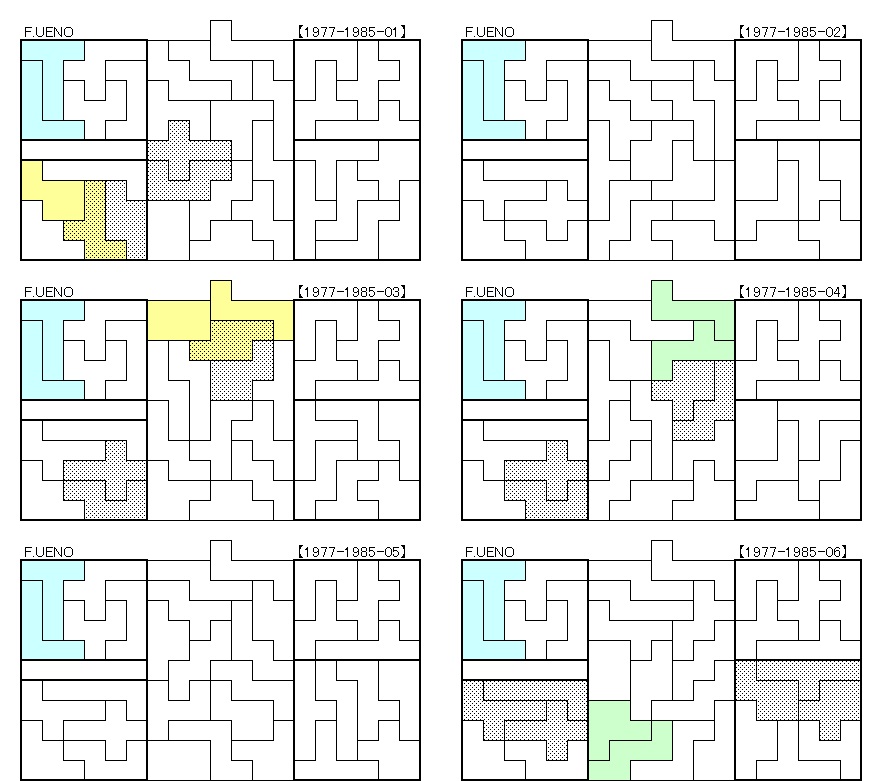
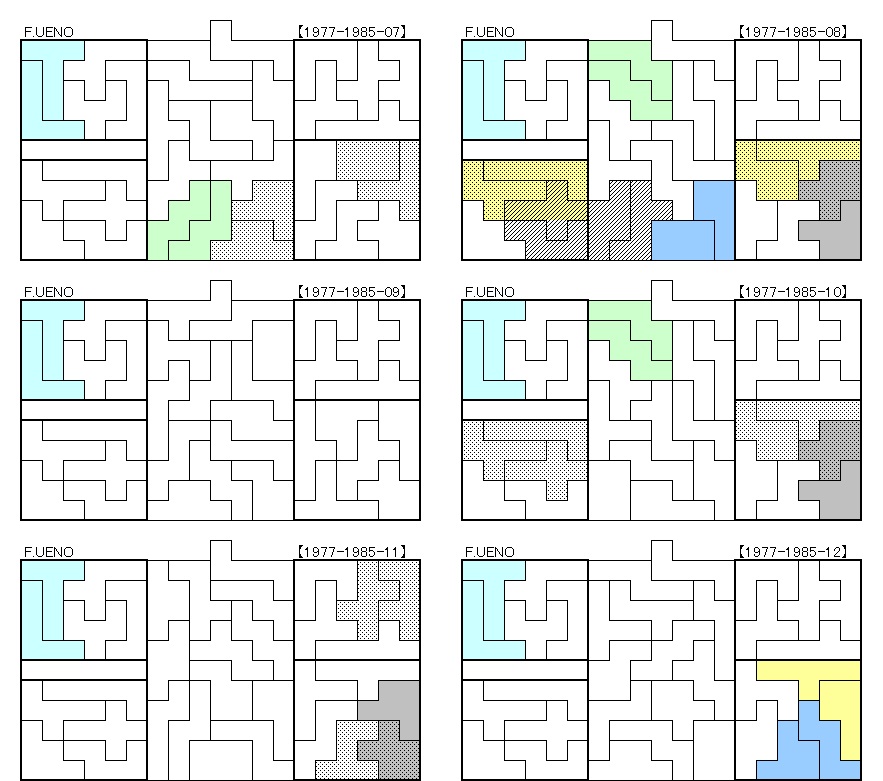
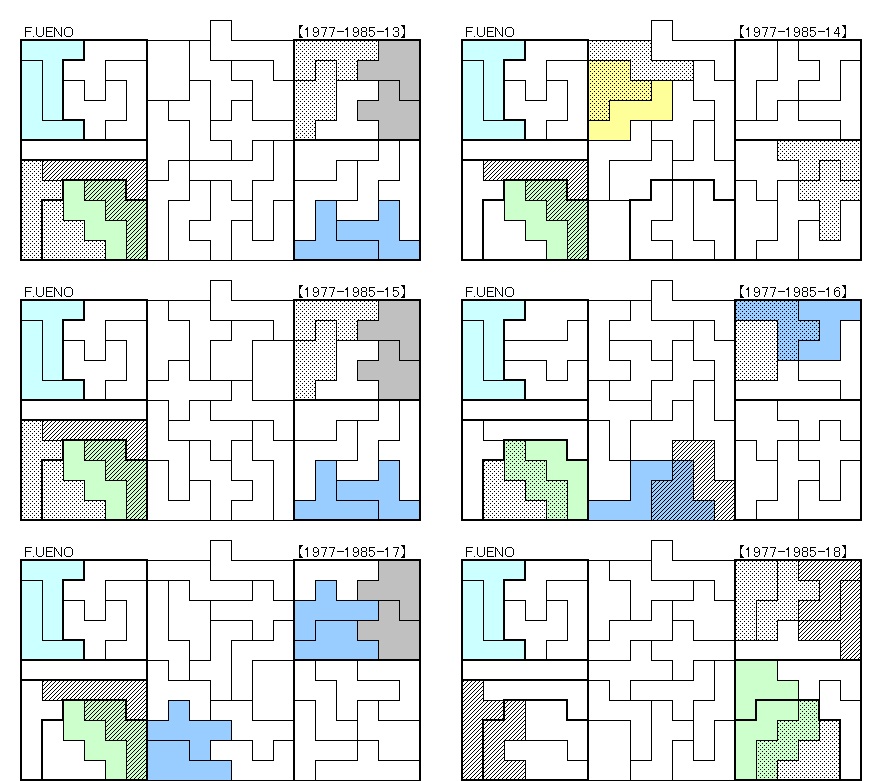
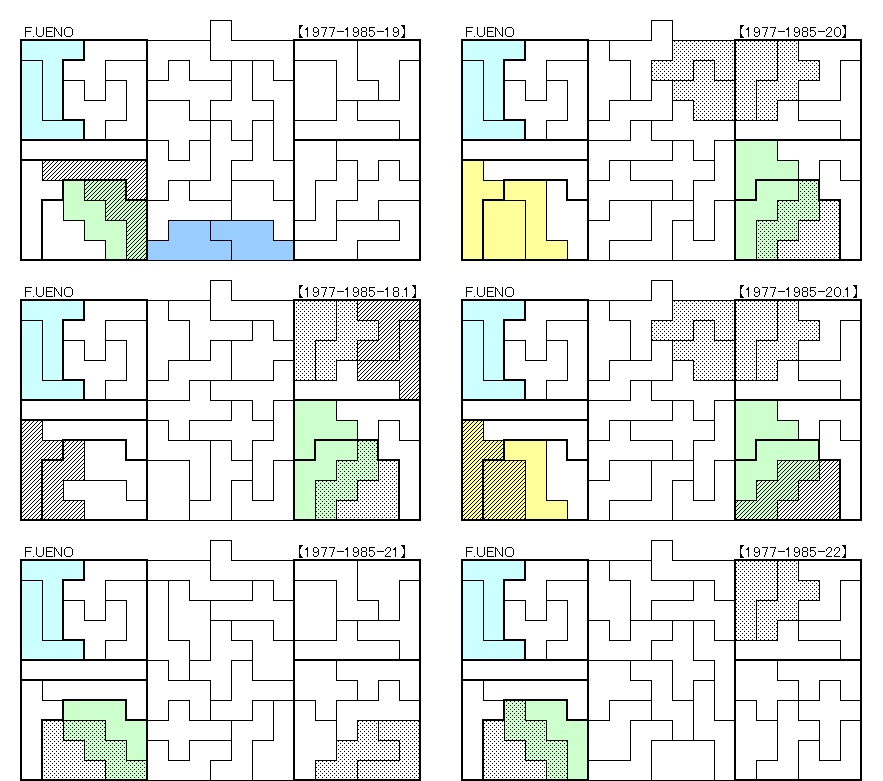
1977年～1985年 22解＋2解
 |
 |
 |
 |
2008年11月30日 1解
2008年12月4日 1解
2008年12月7日 1解
2011年6月19日 1解
2011年7月19日 1解
2011年7月25日 1解
 |
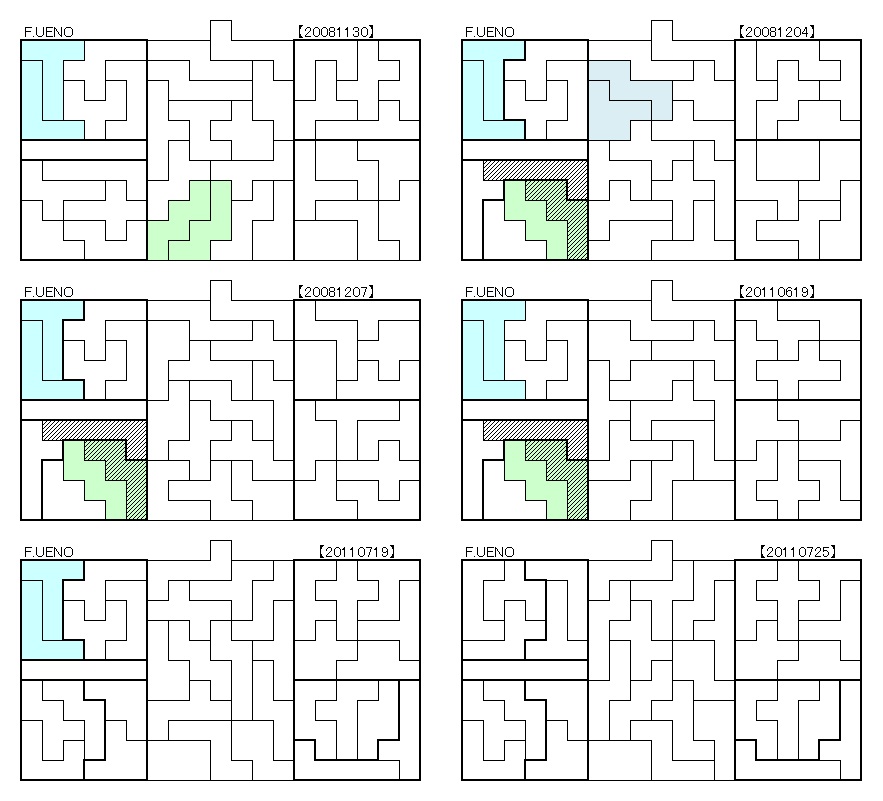■カバン型3個登場
No.20110719及びNo.20110725の2解は、ちょっと特殊です。
5×6の長方形3個全部にカバン型が3個登場しています。
因みにNo.1977-1985-18, 18.1, 20, 20.1の4解にもカバン型は3個登場していますが、長方形に2個、正方形に1個でした。
どちらもカバン型3個には違いありませんが、No.20110719, 20110725の方が組み合わせが少なそうなので、全パターンを計算できるかもしれませんので、ちょっとチャレンジしてみます。
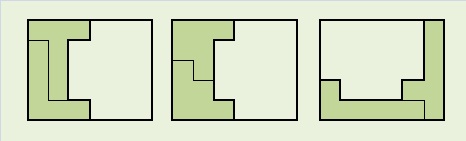まず、カバン型を除くスペースを埋めることができるのは、上記の6ピースだけです。そしてこれ以外にありません。
したがって、全35ピースから上記6ピース及び棒状のピースを除いた28ピースで、カバン型を作ることができるのは何通りあるのか調べます。
その結果は、下記で、27通りです。
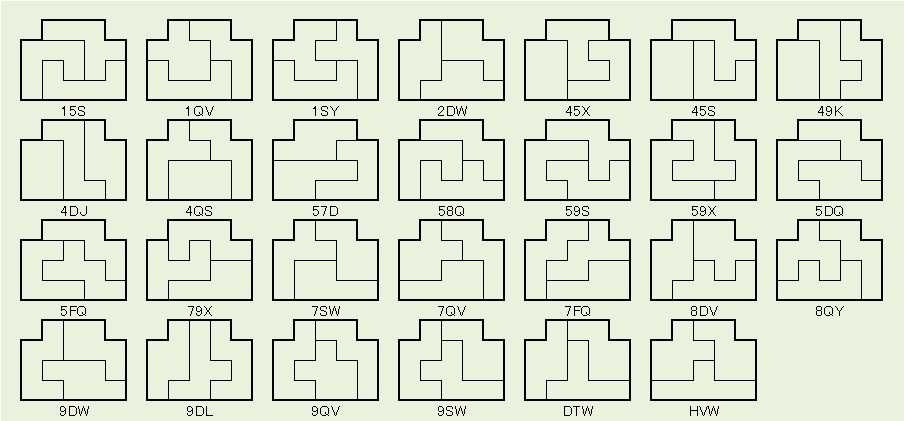
この27通りから3組み取り出す組み合わせは何通りでしょうか？
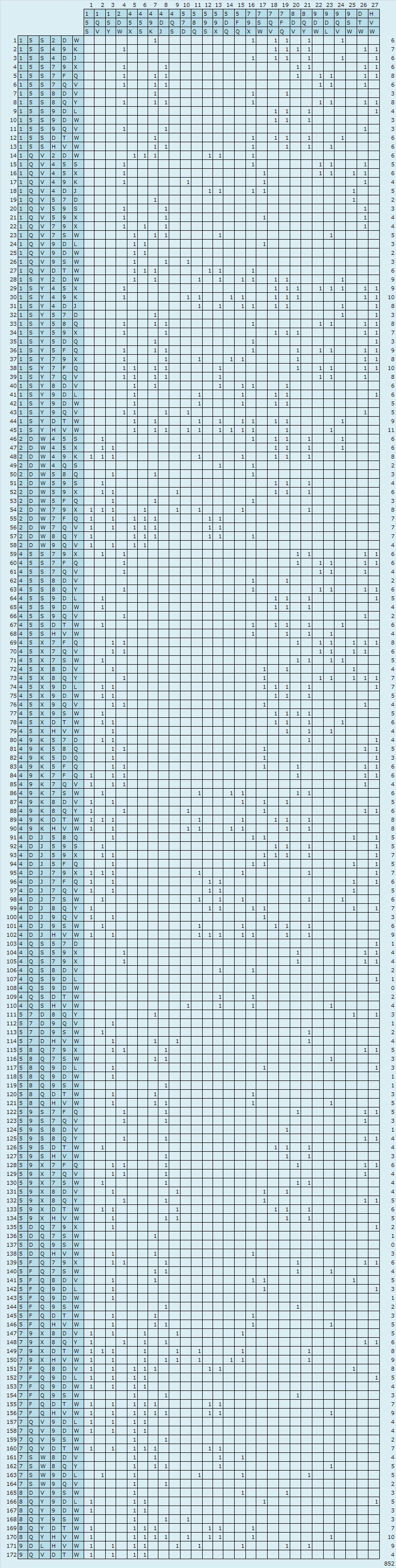
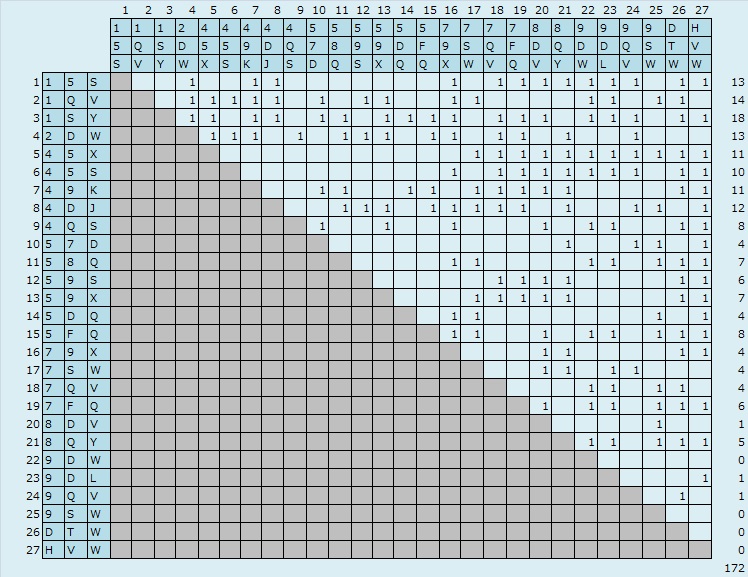
まず2組の組み合わせを考えます。2組を構成するピース（合計6ピース）に重複は許されないので下表のようになり、172通りありました。
計算は、EXCELの数式入力で行いました。左と上の文字をチェックして全部異なれば1, 重複があれば空欄で表しています。
右端の数字は行ごとの小計。小計の最下段にトータルを示しています。その結果172通りということです。
この172通りの組み合わせと、残る1組を組み合わせると、下表のようなります。全部で852通り。
計算は、EXCELの数式入力で行いました。同様に、左と上の文字をチェックして全部異なれば1, 重複があれば空欄で表しています。
右端の数字は行ごとの小計。小計の最下段にトータルを示しています。その結果852通りということです。
