arigirisu2014-NumberPlace

1.解の総数を求める

※このページは、「数独の解生成と解に対する番号付け　戸神　星也　2007年2月」を参考にしています。

3×3数独の解の総数（＝N₀とする）は、6,670,903,752,021,972,936,960=6.67×10²¹であることがわかっています。
どうやって数えたのでしょうか？

ここで用いる記号及び用語は、上記論文「数独の解生成と解に対する番号付け」に従います。

【定義2.1】	3×3数独の解全体の集合をSUDOKUと表す
【定義2.2】	解の総数N₀=\|SUDOKU\|とする
【定義2.3】		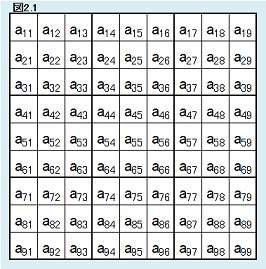3×3数独内の枠で囲まれた部分をマスと呼ぶ。3×3数独の場合は81のマスが存在する。また、マスに図2.1のようなラベルを付ける。例えばa₅₄は3×3数独の第5行第4列のマスを指す。
【定義2.4】		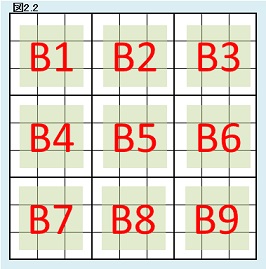3×3数独内の太枠で囲まれた3×3の部分をブロックと呼ぶ。3×3数独の場合は9のブロックが存在する。また、ブロックに図2.2のようなラベルを付ける。 Biと表記されているブロックを第iブロックと呼ぶ。（i=1,2,3,…,9)
同型変換		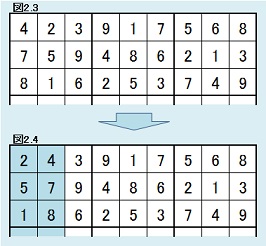上3行が図2.3のような解の総数をMとする。このとき、上3行が図2.4のような解の総数もまたMである。なぜなら、図2.3の1列目と2列目を入れ替えたものが図2.4であり、図2.3の解総数Mが計算で求められているとき、図2.4の解総数をわざわざ計算しなくともMであることは自明であるからである。このようにして、計算すべき対象を狭める手法を同型変換と呼ぶ。

【定理2.5】		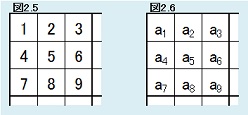第1ブロックの数字を図2.5のように固定することを考える。任意の{a₁,a₂,…,a₉}={1,2,…,9}について、第1ブロックが図2.6と同じ形になっている解総数と、第1ブロックが図2.5と同じ形になっている解総数Aは同じである。
このことから、第1ブロックが図2.5となっている解総数Aが計算できれば、第1ブロックが図2.5以外の解は計算不要であることがわかります。具体的に、どれぐらいの場合について計算不要になるのでしょうか？図2.6は、1～9の数字を重複なく並べる組合せ数なので、9!=362,880通り。因みに図2.5は、この362,880通りの中の1つということです。したがって、解の総数N₀は、図2.5だけの解総数Aの362,880倍ということになります。 N₀=362880A

以上から、以降、第1ブロックは、図2.5で固定して考えます。

■第2ブロック内に対する変換

【定理2.6】		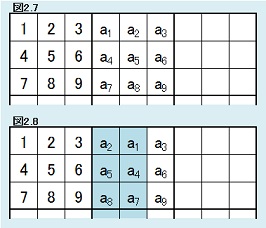第1ブロックは固定。任意の{a₁,a₂,…,a₉}={1,2,…,9}について、第2ブロックが図2.7と同じ形になっている解総数と、第2ブロックが図2.8と同じ形になっている解総数は同じである。
【定理2.7】		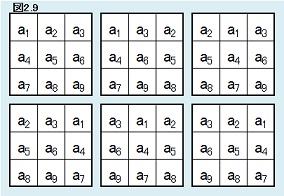【定理2.6】を拡張すれば、任意の{a₁,a₂,…,a₉}={1,2,…,9}について、第2ブロックが図2.9の6パターンのいずれかと同じ形になっている解総数と、第2ブロックが図2.9の他のいずれかと同じ形になっている解総数は同じである。
このことから、第1ブロックが図2.5となっている解総数Aは、さらに第2ブロックが図2.9の6パターンに分けられ、そのうち一つの解総数をBとすれば、A=6Bということになります。 A=6B ∴N₀=362880×6B →第2ブロックについての考察

■第3ブロック内の変換

【定理2.8】		任意の{a₁,a₂,…,a₉}={1,2,…,9}について、第3ブロックが図2.9の6パターンのいずれかと同じ形になっているパターンの解総数と、第3ブロックが図2.9の他のいずれかと同じ形になっているパターンの解総数は同じである。
このことから、第2ブロックが図2.9の6パターンの一つとなっている解総数Bは、第3ブロックが図2.9の他のいずれかと同じ形になっているパターン解総数をCとすれば、B=6Cということになります。 B=6C ∴N₀=362880×6×6C

■ブロックに対する変換

【定理2.9】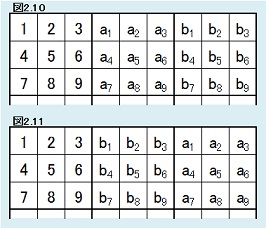

任意のa₁,a₂,…,a₉,b₁,b₂,…b₉({a₁,a₂,…,a₉}={1,2,…,9},{b₁,b₂,…b₉}={1,2,…,9})について、第2、第3ブロックが図2.10と同形になっている解総数と、第2、第3ブロックが図2.11と同形になっている解総数は同じである。

→topに戻る　 →ナンプレtopに戻る
更新：2013年6月7日
最終更新：2013年6月13日