arigirisu2014-Physics

高校物理 Physics for High School

家を整理していたら昔の物理の問題集を見つけました。
まじめにやってたなあ！と思い、今の不真面目さを見つめなおすために、もう一度、この問題集にチャレンジしてみようと思います。（2013.9.24）

なお、この問題集のことは当時(1977.9.21)、通信教育の合格体験記の中で紹介していました。

第１章　力学　　（→目次に戻る）

§１　質点の運動

(1)運動の決定
ある物体の運動状態を決定するには、任意の時刻における位置と速度（加速度）がわかればよい。

(2)力
物体の運動状態を変化させたり、物体を変形させたりする原因になる作用を力という。
また、力ベクトルの働いている点を作用点という。

(3)具体的な力
ⅰ)万有引力と重力
2つの物体の間には必ず引き合う力が働く。これを万有引力という。
両物体の質量をm, m'とし、両物体間の距離をrとすれば、その力の大きさは次の式で表される。（万有引力の法則）

つぎに、地球を完全な球とみなし、その質量をM、半径をR、物体の質量をmとするとき、地表にある物体と地球との間に働く万有引力を地表での重力mgという。

ここで、gは重力の加速度と呼ばれ、地表からの高さが地球の半径に比べて十分小さいときは、近似的に一定と見なしうる。

ⅱ)抗力
物体がある面に接しているとき、その面から受ける力を抗力という。
特に、面に垂直な力を垂直抗力という。

ⅲ)すべり摩擦力
物体が静止しているときに働く摩擦力を静止摩擦力という。
垂直抗力の大きさをNとすると、その大きさは次の不等式で表される。

物体が動いているときに働く摩擦力を動摩擦力という。

また、摩擦力の向きは、接している物体に対する相対的な運動方向と逆向きである。

ⅳ)粘性抵抗
物体が流体中を運動するとき、運動方向と逆向きに粘性抵抗を受ける。
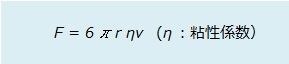
特に半径rの球が速さvで運動するときに受ける力の大きさは次の式で表される。

ⅴ)弾性体に働く力
弾性限界内で、物体のひずみxは、それを起こさせる力の大きさに比例する。（フックの法則）

ⅵ)張力
伸び縮みしないひものとき、ひもの方向に働く。

ⅶ)浮力
流体中の物体は、それが排除する流τの重さに等しい鉛直上向きの力を受ける。
この力を浮力という。（アルキメデスの原理）

ⅷ)圧力
面積Sをもつ平面を考え、この平面に垂直な方向に大きさFの力を加え、この平面をおしたとき、圧力Pはつぎのように定義される。

(4)ニュートンの運動の３法則
第１法則（慣性の法則）
物体に外から働く力の合力が0のとき、物体は静止あるいは等速度運動の状態を続ける。

第２法則（運動の法則）
物体に力が働いたとき生ずる加速度の方向は力の方向と同じで、加速度の大きさは力の大きさに比例し、物体の質量に反比例する。

第３法則（作用反作用の法則）
物体Aが物体Bに力を作用するときは、物体Bもまた物体Aに、同一直線上で大きさが等しく向きが反対の力を作用する。

(5)運動方程式
第1法則と第2法則とを数学的に表現すると、運動方程式を得る。