例題集 第1章 力学
例題1 運動方程式
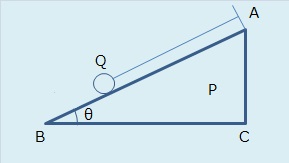 |
図のように水平面に対する傾角がθのなめらかな斜面ABをもった質量Mの物体Pがある。その斜面上に質量mの小球Qをので、これに軽い糸をつけて斜面の上端Aに固定してある。 Pの底面BCもなめらかでPは水平な床の上を自由に滑らすことができる。 重力の加速度をgとして以下の設問に答えよ。 |
(1) Pが床上で静止しているとき、糸の張力およびQが斜面から受ける抗力の大きさはそれぞれいくらか?
 |
Qに働く糸の張力をT1、斜面の抗力をN1とすると、斜面方向と斜面に垂直な方向の力のつり合いの条件より T1-mgsinθ = 0 N1-mgcosθ = 0 ∴T1= mgsinθ = 0 N1= mgcosθ = 0 |
 |
糸の張力をT2、斜面の抗力をN2とすると、Qに対する水平方向と鉛直方向の運動方程式は次のようになる。 N2sinθ-T2cosθ=mα----------------① N2cosθ+T2sonθ-mg=0-------------② ①、②より、 T2=m(gsinθ-αcosθ) N2=m(αsinθ+gcosθ |
(3) (2)において、αがある値αcを越せば
開始:2013年9月27日
更新:2013年10月2日