再帰 Recursion
 |
再帰というのは、アルゴリズムの一つ。 このページは「再帰の技法 基本的考え方・アルゴリズム・プログラミング(2006年11月10日 玉井 浩、エスアイビー・アクセス)」を参考にしています。 |
第1章 再帰の基本 →目次に戻る
1-1.基本的な考え方
階乗
nの階乗n!を求める関数factorialを定義し、「再帰」について考えます。(factorial=階乗)
| nの階乗の定義を関数factorial(n)で表すと、 1) factorial(0)=1 2) factorial(n)=n*factorial(n-1) ただし、nは正の整数 |
 |
| プログラムは下記の通り。 | |
 |
フィボナッチ数列
フィボナッチ数列の各項は、最初の2つの項は1で、以後の項は直前の2つの項の和になっています。
1,1,2,3,5,8,13,21,34,…
フィボナッチ数列の定義を関数fibonacci(n)で表すと、
1) fibonacci(1)=fibonacci(2)=1
2) fibonacci(n)=fibonacci(n-2)+fibonacci(n-1)
ただし、nは3以上の整数
| 第n項目の数がいくつになるか求めるプログラムは下記の通り。 |
 |
ハノイの塔
再帰を説明する参考書には必ず出てくるアイテムです。「ハノイの塔」参照。
1-2.しらみつぶし
あらゆる場合を漏れなく尽くす=しらみつぶし、について考えます。
真理値表
下のような真理表をプログラムで作るにはどうするか?という話です。
| b0 | b1 | b2 | b0 or (b1 and (not b2)) |
| F | F | F | F |
| F | F | T | F |
| F | T | F | T |
| F | T | T | F |
| T | F | F | T |
| T | F | T | T |
| T | T | F | T |
| T | T | T | T |
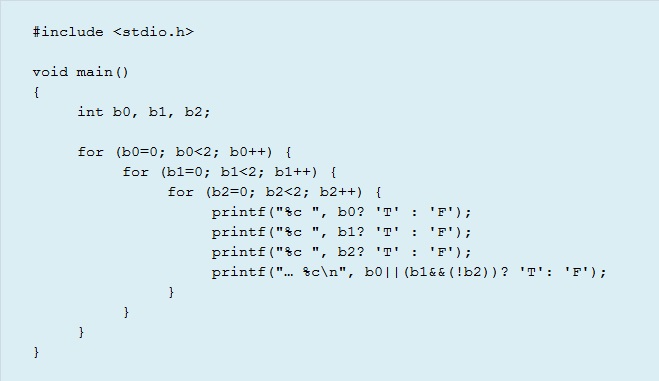
まず、再帰のことは忘れて、普通に考えると下記の様なプログラムになると思います。
 |
 |
変数がb0, b1, b2の3つだけなので、上記のようなfor分のネスト構造でも問題ないですが、n個だったらたいへんです。
そこで「再帰」の登場です。
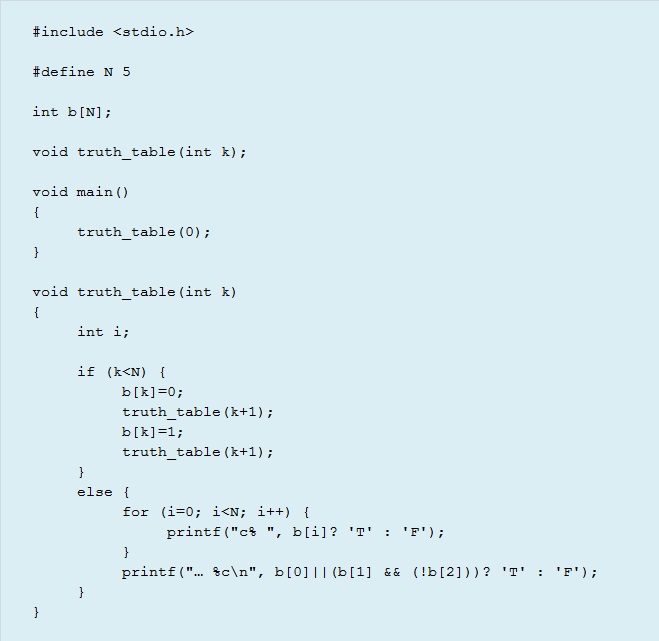
b0, b1, b2は、配列b[0], b[1], b[2],…,b[n-1]とします。
 |
 |
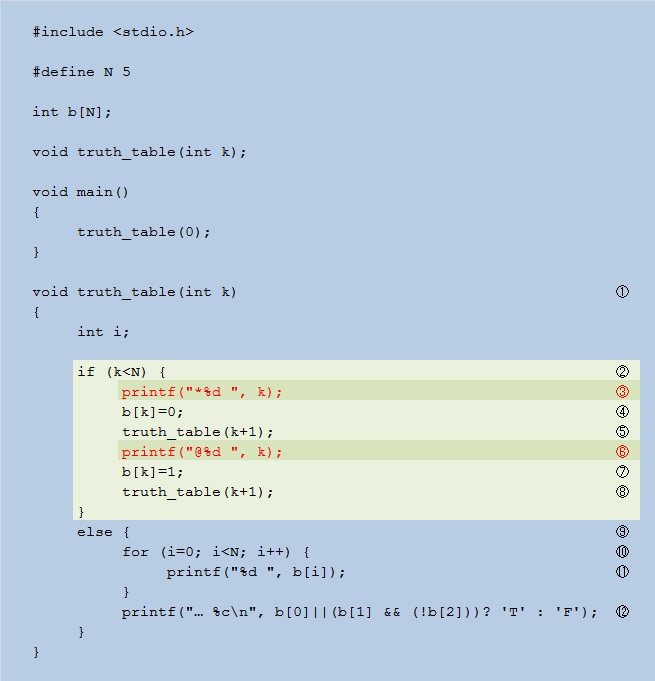
| ほんとうにしらみつぶしできているのでしょうか? 「再帰のところがどのようになっているのか」がわかるように、下記の様に③⑥を追加してみました。 |
|
 |
|
| 【1行目】*0*1*2*3*4に続いて0 0 0 0 0... Fとなっています。 まず①でtruth_table(0)を実行。kの値は0。②に進み、k<N判定で③へ。 k=0なので「*0」を表示後④に進みb[0]に0を与え、⑤で再帰呼び出し。 ①に戻りtruth_table(0+1)を実行。kの値は1。②に進み、k<N判定で③へ。 k=1なので「*1」を表示後④に進みb[1]に0を与え、⑤で再帰呼び出し。 ①に戻りtruth_table(1+1)を実行。kの値は2。②に進み、k<N判定で③へ。 k=2なので「*2」を表示後④に進みb[2]に0を与え、⑤で再帰呼び出し。 ①に戻りtruth_table(2+1)を実行。kの値は3。②に進み、k<N判定で③へ。 k=3なので「*3」を表示後④に進みb[3]に0を与え、⑤で再帰呼び出し。 ①に戻りtruth_table(3+1)を実行。kの値は4。②に進み、k<N判定で③へ。 k=4なので「*4」を表示後④に進みb[4]に0を与え、⑤で再帰呼び出し。 ①に戻りtruth_table(4+1)を実行。kの値は5。②に進み、k<N判定で⑨へ。 ⑩⑪でb[0],b[1],b[2],b[3],b[4]を表示後⑫に進み論理式の結果を表示し、⑥へ。 【2行目】 k=4なので「@4」を表示後⑦に進みb[4]に1を与え、⑧で再帰呼び出し。 ①に戻りtruth_table(4+1)を実行。kの値は5。②に進み、k<N判定で⑨へ。 ⑩⑪でb[0],b[1],b[2],b[3],b[4]を表示後⑫に進み論理式の結果を表示し、⑥へ。 (つづく) 最終更新2013年6月3日 |
 |