arigirisu2014-Tetromino

テトロミノ Tetromino

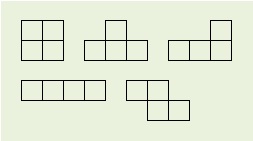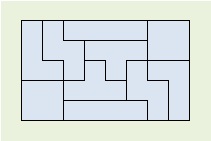
4個(Tetra)の正方形(Omino)の組合せでできる5種類のピース(piece)を2個ずつ、計10個を箱(5×8)に詰めるパズルを、テトロミノといいます。入れ方は783通りあります。この783通りをコンピュータに計算させます。

※このページは「実践Ｃプログラミング～パズルとゲームのアルゴリズム」東京大学　小野芳彦著　工学社　昭和61年12月20日初版発行を参考にしています。

パズルの木

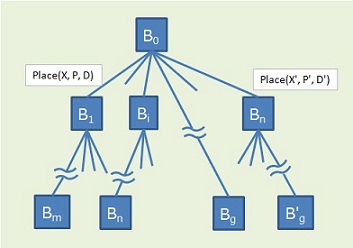ピース(piece)が詰められている箱(board)の状態(state)を B_i と書くことにします。そうすると、初期状態である空の箱 B₀ から全部詰まっている状態 B_g (ゴール状態と呼ぶ）への道筋を求めることが解を求めることになります。
もちろんB_g がたくさん存在することもあります（テトロミノでは783解、存在する）。
B_iでピース X を場所 P に D の方向に置くと B_j とう状態になるというような関係を図に示すと左のような木になります。
結局、パズルを解くことは木をサーチすることと同値であることになります。

深さ優先サーチ

深さ優先(depth-first)サーチは、木を深く深く探すサーチで、運がよいときは最も早く、また最も手軽に解を求めることができるやり方です。

(1)B0をstateの初期値に設定する。
(2)stateがゴールであれば解が見つかった。終了。
(3)stateがゴールでなければ、未だ試していない可能な手があるか調べる。
(4)可能な手がなければ失敗なので1つ前のstateに戻して、(3)へ行く（バックトラックと呼ぶ）。
(5)可能な手を1つ実行してstateを変え、(2)へ行く。

これを疑似的なプログラムに書くとリスト1のようになります。

リスト1
struct STATE state = B0; /*(1)*/
main()
{
while(!isgoal(state)) /*(2)*/
{
puthand(); /*(3)*/
while((m=gethand()) == EMPTY) /*(3)*/
backtrack(); /*(4)*/
pushstate(m); /*(5)*/
}
}

puthand()
{
/*stateで可能な手すべてをhandキューに入れる*/
}

gethand()
{
/*handキューから手を１つ取り出す*/
/*空になったらemptyを返す*/
}

isgoal(state)
{
/*ゴールでなければ0を返す*/
}

pushstate(select)
{
/*stateとhandキューをスタックする*/
/*selectされた手を実行してstateを変える*/
}

backtrack()
{
/*stateとhandキューをスタックから戻す*/
}

リスト2
main()
{
Dsearch(B0);
}

Dsearch(state)
{
struct STATE state;
{
struct HAND m;
if(isgoal(state);
{
printgoal(state);
exit(0);
}
puthand();
while((m=gethand())!=EMPTY)
Dsearch(do_hand(state,m));
}
struct STATE do_hand(state,m)
struct STATE state;
struct HAND m;
{
/*stateに手mを実行して、その結果の状態を返す*/
}
}

アルゴリズムの(4)と(5)の部分を実行するために、かなり面倒なプログラム(pushstateとbacktrack）を必要としますが、自分自身を呼び出すリカーシブ・コール（再帰呼び出し）でこのバックトラックを実現することができて、プログラムの見通しが良くなります（リスト2）。

boardの定義

箱(board, 5×8)は、下記のように定義します。下辺と右辺に壁（枠）を作っています。

構造体PIECEの定義(PIECE型の定義)

◆PIECE型を定義します。

struct PIECE {
char name; /*ピースの名前 */
int dirs; /*ピースによって置き方が何通りか存在します（最大は8通り） */
int free; /*未使用のピース数（最初は2） */
int disp[8][4][2]; /*pieceの左上を0番地とし、他の正方形（omino)の番地は相対的に表現します。*/
}

◆PIECE型の変数pcsを定義します。
struct PIECE pcs[5] = { /* ピース(piece)は全部で5種類。それぞれO, I, T, Z, Lという名前を付けます */
{'O', 1, 2, 0,0, 0,1, 1,0, 1,1 },
{'I', 2 ,2, 0,0, 0,1, 0,2, 0,3,
0,0,1,0, 2,0, 3,0 },
{'T', 4,2,