素数 Prime Number
1と自分自身以外に約数をもたない自然数のうち1でないものを素数といいます。目次
| 素数が無数に存在することの証明 | |||
| 素数を求めるプログラム | |||
| 高速化 | |||
| エラトステネスのふるい | |||
| エラトステネスのふるいを使って素数を列挙するプログラム | |||
| 素因数分解の一意性 |
素数が無数に存在することの証明
ユークリッドの「ストイケイア(Stoikheia)」で「素数は無数に存在すること」が証明されているそうです。→目次に戻る※出典:Yahoo!百科事典
| ■証明 素数が有限個であると仮定します。 その集合をP = {2, 3, 5, …, q, p}とします。(一番大きな素数をpとします。) ここで、N = 2×3×5×…×p + 1という数を考えます。Nはpより大きいのは明らかですので集合Pには属しません。 このNをすべての素数すなわち2, 3, 5, …, pで割ってみると、すべて余り1となり、割り切れません。 N÷2=3×5×…×q×p余り1 N÷3=2×5×…×q×p余り1 N÷5=2×3×…×q×p余り1 … N÷p=2×3×5×…×q余り1 したがって、Nは1と自分自身以外に約数をもたないことになりますから、Nは素数です。 これは、一番大きいはずの素数pより大きな素数Nが存在することになり矛盾します。 よって素数は有限個ではない、すなわち無数に存在することになります。(証明終わり) |
素数を求めるプログラム
素数を求めるにはどうしたらいいのでしょうか?→目次に戻るまずは、真面目に、定義通り、「自分自身より小さい数字で割り算して、約数がなければ素数と判定する。」というプログラムを書いてみます。(ブルーのところは処理時間測定のために書き加えた部分です。)
配列primeの添字の数字が素数かどうか判定する対象です。判定結果(素数なら0, それ以外は1)が配列に格納されます。
最終的に0が格納されているものだけを選んで、その添字の数字を表示させています。

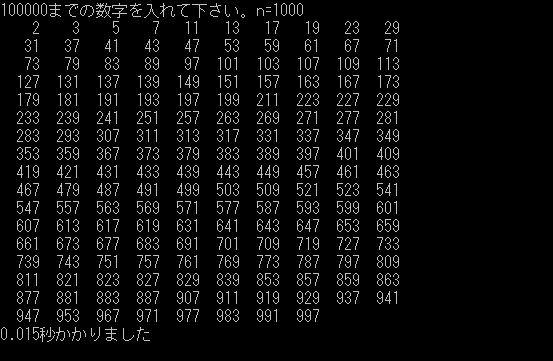
このアルゴリズム(素数の定義のままで何も考えていないのでアルゴリズムといえるかどうかは疑問だが)は、nが大きくなるにつれ、表示にかかる時間が気になってきます。
n= 10000(=104)のとき、表示までに 0.257秒かかりました。
n=100000(=105)になると表示までに17.908数かかりました。
たぶんn=106になると表示まで待っていられないと思います。
もう少し高速化を図りたいものです。
→目次に戻る
高速化
まず、2以外の偶数は素数でないので、配列primeの添字iが偶数(2の倍数)なら、prime[i]=1にします。3の倍数も素数ではないので、iが3の倍数なら、prime[i]=1にします。
要するに、前のプログラムでは自分自身より小さなすべての数字で割り算してみて、余りが0かどうか判定していましたが、この処理を行う回数を事前に少なくしておこうというわけです。
とりあえず2の倍数、3の倍数を除外しておくとどれぐらいスピードがあがるでしょうか?→目次に戻る

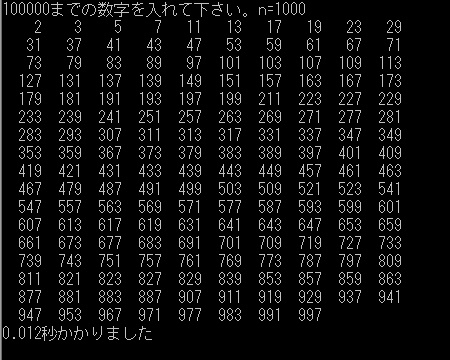
n= 10000(=104)のとき、表示までに 0.257秒だったものが0.141秒へ。
n=100000(=105)になると表示までに17.908数だったものが6.494秒にまで縮まりました。
| n | 表示までの時間(秒) | |
|---|---|---|
| 定義通りのプログラム | 2の倍数、3の倍数を 事前に除外したプログラム |
|
| 101 | 0.000 | 0.000 |
| 102 | 0.002 | 0.002 |
| 103 | 0.016 | 0.012 |
| 104 | 0.257 | 0.141 |
| 105 | 17.908 | 6.494 |
エラトステネスのふるい
たとえば100までの素数を知りたいとします。→目次に戻るその時は100の平方根=10までの素数の倍数をつぎつぎに除外していきます(ふるい落とします)。
10までの素数は 2, 3, 5, 7
です。
まず、1 は(特別な数で素数ではないので)消してしまいます。
次に、2は(素数ですから)そのままにして、
2の倍数の 4, 6, 8, 10, 12, …, 100
をふるい落とします。
同じようにして、
3の倍数の 6, 9, 12, 15, 18…
5の倍数の 10, 15, 20, 25, 30, …
7の倍数の 14, 21, 28, 35, 42, …
をつぎつぎにふるい落としていきます。
そのとき、ふるい落とされずに残った数が素数だというのです。
残ったのは
2,3,5,7,11,13,17,19,23,29,31,37,41,
43,47,53,59,61,67,71,73,79,83,89,97
です。
11
31
41
61
71
※エラトステネス(Eratosthenes)は紀元前3世紀ごろのギリシアの天文学者・地理学者で、地球の全周を計算した人です。
この方法はそのころすでに発見されていたものと思いますが、現代でも基本的にはこの方法を改良して素数表をつくっているということです。
| ■エラトステネスのふるいの証明 さて、どうしてふるい落とされずに残った数が素数だといえるのでしょうか。 ふるい落とされずに残った数Qについて考えてみます。(10<Q≦100) もし、Qが素数でなく、合成数だったら Q=p1×p2×… のように素因数分解されます。(p1, p2, ・・・は素因数。合成数なら素因数は2個以上あります。) ところでp1, p2, …のすべてが100の平方根=10よりも大きいと仮定すると、 Q=(10より大きい数)×(10より大きい数)×… というわけですから、Qが100より大きくなり矛盾。 したがって、p1, p2, …の少なくとも一つは100の平方根=10までの素数ということになります。 その素数をp1とします。そうすると、 Q=p1×(p2×…) となります。これは、Qがp1の倍数であることを意味します。p1は100の平方根=10までの素数ですから、その倍数であるQはエラトステネスのふるいで除外されているはずです。 ところが、Qはふるい落とされずに残っており矛盾。 よってQは合成数ではなく素数であるということになります。(証明終わり) |
エラトステネスのふるいを使って素数を列挙するプログラム
このアルゴリズムを使うともう少し高速化できそうです。→目次に戻る前回のプログラムではnまでの数字について、事前に2の倍数と3の倍数を除外し、残った数に関しては定義通り、自分自身より小さいすべての数で割り算し、すべてで割り切れなければ素数と判定しました。
エラトステネスのふるいを使うと、つぎのようになります。
①1を除外する
②残った整数のなかでもっとも小さな数字(=2)の倍数を除外する
③これをnの平方根を超えない最大の整数kまで続ける(3, 5, 7, 11, 13,…,k)。
④残った数がnまでのすべての素数である。
プログラムは以下のようになります。

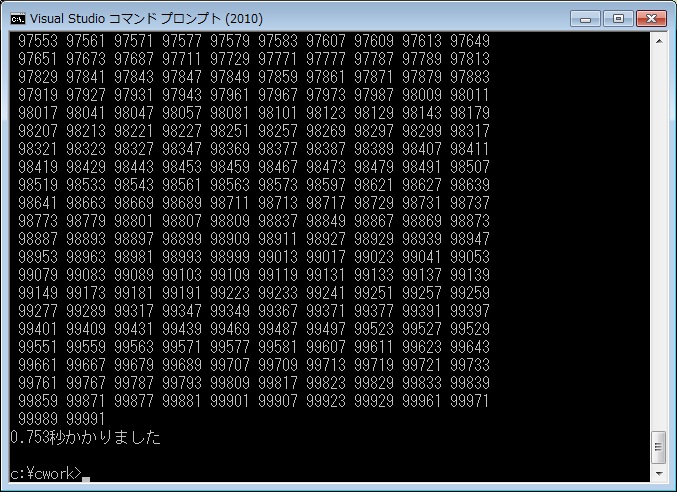
| n | 表示までの時間(秒) | ||
|---|---|---|---|
| 定義通りのプログラム | 2の倍数、3の倍数を 事前に除外したプログラム |
エラトステネスのふるい を使ったプログラム |
|
| 101 | 0.000 | 0.000 | 0.000 |
| 102 | 0.002 | 0.002 | 0.002 |
| 103 | 0.016 | 0.012 | 0.013 |
| 104 | 0.257 | 0.141 | 0.084 |
| 105 | 17.908 | 6.494 | 0.753 |
n=100000(=105)のように大きな数字になると、とても高速になることがわかります。
→目次に戻る
素因数分解の一意性
素数を見つける、あるいは素数かどうか判定するのは非常に手間がかかることがわかりました。→目次に戻る一方、合成数とわかったら、素因数に分解できるわけですが、これがただ1通りであるというのはなぜなんでしょう?
いろいろ調べましたが、難しいから省略しているものがほとんど。
しかし、やっとわかりやすく解説したものを見つけましたので紹介します。
証明の方針は下記の2ステップです。
1)数学的帰納法を使って、すべての自然数が因数分解できることを証明する。
2)次に背理法を使って(2つ以上存在すると仮定して)矛盾を指摘する。
■すべての自然数について因数分解できることの証明
たとえば、10までの自然数はすべて因数分解できる。
そこで、ある自然数Nまでは素因数に分解できると仮定する。
このときN+1について考える。
ⅰ)N+1が素数のとき
N+1を素因数として因数分解できる
ⅱ)N+1が合成数のとき
合成数の定義によってN+1=abと2以上の自然数aとbの積に分けられる。
このとき、a, bは明らかにN以下の自然数なので、仮定よりそれぞれ因数分解できる。
よってabも因数分解できる。すなわちN+1も因数分解できる
ⅰ)ⅱ)より、すべての自然数について因数分解できる。
■因数分解の一意性の証明
①まずpを素数とし、pa=bcが成立すれば(a, b, cは自然数)、pはbまたはcの約数になるといえるか調べます。
pa=bcの両辺をpで割ると
a=bc / p
左辺は自然数ですから、右辺も自然数。
ここで、bとcの両方がpの倍数でないと仮定すると、bcは因数にpを含みませんのでbcはpで割り切れなくなり、右辺は自然数にならず矛盾します。
よって、bとcのどちらか一方はpの倍数です。すなわち①は成立します。(証明おわり)
②同じくpを素数とし、pa=bcdが成立すれば(a,b,c,dは自然数)、pはb, cまたはdの約数になるといえるか調べます。
pa=bcdの両辺をpで割ると、
a=bcd / p
左辺は自然数ですから、右辺も自然数。
ここで、b,c,dのすべてがpの倍数でないと仮定すると、bcdは因数にpを含みませんのでbcdはpで割り切れなくなり、右辺は自然数にならず矛盾します。
よって、b,c,dのどれか一つはpの倍数です。すなわち②は成立します。
③同様にして、
pa=b1b2b3…bnが成立すれば、b1, b2, b3, …, bnのどれかはpの倍数である、ということが任意のnについて成立します。
さて、いよいよ一意性の話になります。
任意の自然数Nが、素数の2通りの組み合わせp1, p2, p3, …, pmと、q1, q2, q3, …, qnに因数分解されたと仮定します。
すなわち、
N=p1p2p3…pm=q1q2q3…qn
と2通りに表されたと仮定します。
③より、q1, q2, q3, …, qnのどれかは、素数p1の倍数といえます。仮にqkが素数p1の倍数だとすれば、
qk=tp1 (tは自然数)
ところで、qkは素数ですから、上記より t=1, qk=p1となります。
このようにして、p2, p3, …, pmについて確認していくと、最終的に
p1=q1, p2=q2, p3=q3, …, pm=qnで、m=n
が成立します。
ということは「素数Nが2通りの組み合わせに因数分解される」という仮定に反します。
よって、素数Nは1通りの組み合わせしかなく、素因数分解の一意性が証明されました。(証明おわり)
→目次に戻る