RSA暗号 RSA Cipher

いきなりRSAといっても何だかわかりませんね。 現代の暗号にもっとも大きな影響を与えた暗号システムのことで、このシステムを開発した3人(リヴェルト、シャミア、アドルマン)の頭文字をとって名付けられたものです。（→暗号解読） このシステムにおいて、「素数」はきわめて重要な役割を担います。素数が現代のセキュリティを守っているといわれる所以です。さて、どのように現代セキュリティ（暗号化）に素数が関わるのでしょうか？

たとえば、適当に２つの素数を選んでみます。
 p=99,119、 q=99,991とでもしましょう。
ここでp×qを計算してみます。すると、pq=9,911,007,929が得られます。
われわれは、9,911,007,929という数字がpとqを掛け合わせて出てきたことを知っていますが、いきなり9,911,007,929という数字が出てきたら、これが素数なのか合成数なのかわかりません。
そこで、コンピューターの登場。
さて、この数字が素数なのか、合成数なのかを調べるには、基本的にエラトステネスのふるいを使ったアルゴリズムを使うのが最も効率的ですので、まず、9,911,007,929の平方根を求めます。
電卓をたたくと99,554.04…ですから、99,554までの素数を見つけて、その倍数を除外すればいいことになります。

9,911,007,929という数字は大体10¹⁰に近い数字ですから、コンピュータでもかなり時間がかかることがわかります。
セキュリティに応用する場合には、10¹⁰などという遠慮した大きさの数字ではなく10³⁰⁸などというとてつもなく大きな数字を使って、pとqの２つを特定されにくくするわけです。
「暗号解読」によれば100MHz Intel Pentium搭載機でRAMが8MBの場合、10¹³⁰程度の数を素因数分解するには、ざっと50年かかるそうです。
しかし、世界中のコンピュータ1億台のパソコンを使って計算すると15秒ほどで因数分解できてしまうそうで、そのため、確実にセキュリティを保証するためには、もっと大きな素数を使うのだそうです。なんと心配性なんでしょうか。
重要な銀行取引では少なくとも10³⁰⁸程度の数を使うそうです。これぐらい大きくなると、さすがに1億台のパソコンを駆使しても1千年以上かかるとのこと。これなら安心というわけです。

しかし、arigirisu的には、ここに大胆な予言をせざるを得ません。素数を見つけるアルゴリズムは紀元前3世紀に見つけたものから発展していないのです。そろそろ、308桁だろうがなんだろうが、数字を入力するだけで即座に素数か合成数か判定するアルゴリズムが見つかるはずです。これを「arigirisuの予測」と呼ぶことにします。フェルマーの最終定理も解けました。きっとarigirisuの予測も解決されることでしょう。

鍵配送問題

遠く離れた、まだ一度も合ったことのない二人の人間が秘密文書をやりとりしたいとき、送信者はその文書を暗号化します。
このとき、送信者は暗号化するためには、鍵を使います。
一方、受信者は暗号化された文書を鍵を使って復元します（復号といいます）。
さて、この鍵はどうやって共有するのでしょうか？まだ一度も合ったことがないのです。
たぶん、この鍵も「秘密文書」として送ることになるはずですが、、、、これはジレンマです。 これを「鍵配送問題」といいます。
鍵配送問題を考えるときは、アリス、ボブ、イブという三人の架空の人物に登場願うのが、慣例のようですので、ここでもそうします。アリスがボブに、またはボブがアリスにメッセージを送ろうとし、イブがその盗聴を試みます。

以下に、鍵配送問題の解決事例を示します。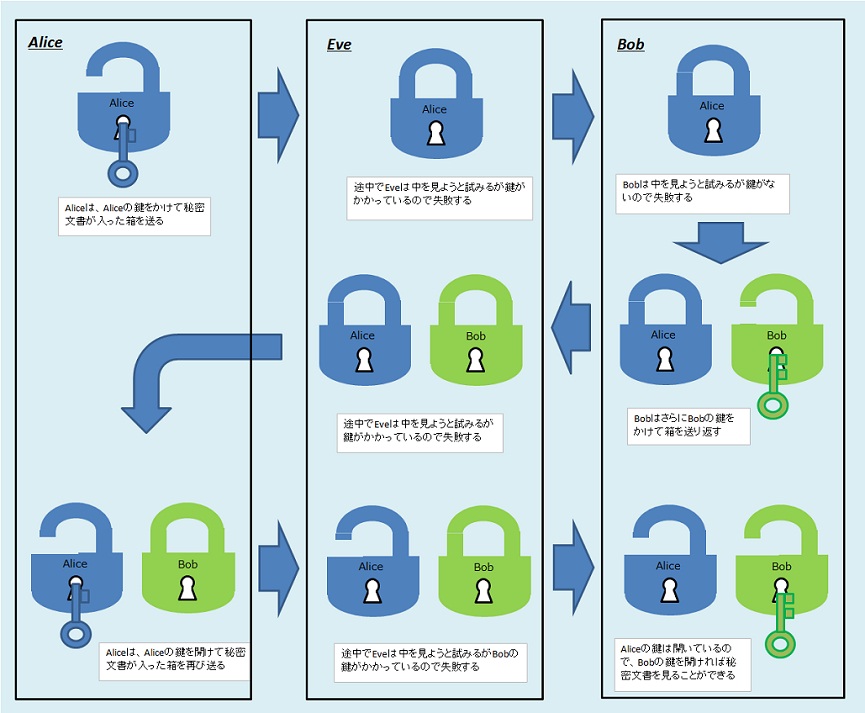

RSAの数学

※この項目は「暗号解読」の補遺Jを参考にしています。

以下は、RSAによる暗号化及び復号に関する簡単な数学的説明です。
メッセージMを暗号化したものをCとします。MもCも数字です。
(1)Aliceは大きな素数p, qを選び、その積N=pqを求める。
   例えばp=11, q=17, ∴N=187とします。
(2)Aliceはgcd(e,(p-1)×(q-1))=1となるeを適当に選ぶ。(gcd：最大公約数）
　要するにeと(p-1)×(q-1)は互いに素という意味です。
　p=11, q=17とすると、(p-1)×(q-1)=10×16=160です。
　eは、160と互いに素となる数ならなんでもかまいません。
(3)Aliceはed≡1(mod (p-1)(q-1))となるdを求める。
   160で割って1余るようにe, dを決めてみます。
　ed=161にしてみます。
　eは(2)の条件を満たしていればなんでもいいので7にしてみます。
　するとd=161÷7=23になります。
(4)AliceはN, eを公開鍵として公開し、dを秘密鍵として秘密に保持する。
(5)AliceにメッセージMを送りたいときは、公開鍵Nとeを使って次の数式にしたがって暗号化する。
    C=M^e(mod N)
たとえば、BobがメッセージM=88をAliceに送りたいとします。
　C=88⁷(mod 187)
さてこれをまともに計算すると、、、88⁷=40,867,559,636,992
これを187で割ると、40,867,559,636,992÷187=218,543,099,663余り11
   ∴C=11
(6)BobはAliceに暗号文C(=11)を送ります。
この時点でC(=11)から即座にM(=88)は、EveにもAliceにも求められません。
(7)復号するにはAliceは次の数式を用いる。
    M=C^d(mod N)

■具体例
    C=11, d=23, N=187を代入すると
    M=11²³(mod 187)
ここで、もう11²³を計算することができなくなってしまいました(桁数が大きくなりすぎてエクセルの対象範囲外)。
モジュラ算術の登場です。
次のようになります。23=1+2+4+8+8なので
    M=11²³(mod 187)
      =[11¹(mod 187)×11²(mod 187)×11⁴(mod 187)×11⁸(mod 187)×11⁸(mod 187)](mod 187)
      =(11×121×55×33×33)(mod 187)
      =79,720,245(mod 187)
      =88
めでたくAliceはBobが送ったM=88を解読できました。

■M=C^d(mod N)の証明
いよいよ、C=M^e(mod N)のとき、なぜM=C^d(mod N)になるかの証明です。
もともとの文を平文（ひらぶん）といいます。暗号化した文を暗号文といいます。
Bobは公開されているeとNを使って平文Mを暗号文Cに変換します。
dはAliceだけの秘密鍵です。
Aliceは、暗号文CをdとNを使って平文Mを得ますが、直接Nを使うのではなく、Aliceだけが知っているp, qも必要になるというところがミソです。