→topに戻る →目次に戻る 2.2.1 ゲームの木へ戻る← →2.3 ゲームの木の探索---先読みのプログラム---へ
2.2.2 局面の表現方法
ここでは、ゲームの局面状態をコンピュータで表現する方法(コンピュータにわかってもらう方法)を具体的に述べます。盤の表現には、配列を使うのが便利です。
2次元配列を用意し、配列の一つの要素で、ひとつのマスの状態を表すのが最も自然です。
【盤を2次元配列で表す】
 |
というように、リバーシの3つの状態を定義し、
 |
と盤の配列を宣言します。
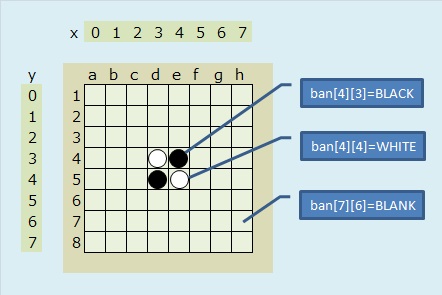 |
盤面を初期化するプログラムは下記の様になります。
 |
更新:2013年6月18日
【盤を1次元配列で表す】
さて、上記のように盤は2次元配列で表すとわかりやすいのですが、高速性を要求されるリバーシのプログラムでは、2次元よりも1次元配列を使う方が有利とのこと。
そこで、盤を1次元配列で表すことを考えます。
2次元配列banを1次元配列に対応させるためには、以下の変換式を用います。
ban[x][y] = ban[pos]
= ban[x+y*9] (pos=x+y*9, 1<=x<=8, 1<=y<=8)
逆に、盤上の位置posからx, yを得るには、
x=pos%9
y=pos/9
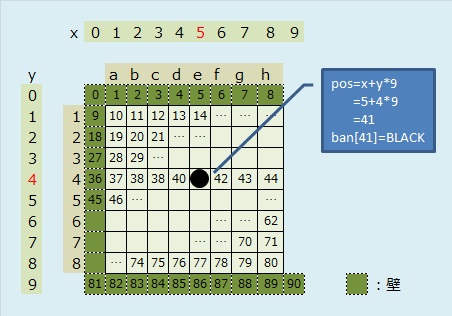 |
また、
 |
と宣言しておいて、端の判定に使います。
盤面を初期化するプログラムは下記の様になります。
 |
これで、リバーシの座標x,yと石の色を代入すれば、配列を使ってどのような局面でも表現できることになります。
更新:2013年6月28日