→topに戻る　→代数topに戻る  →目次に戻る

約数の個数と総和

問題３

（１）1050の正の約数の個数nを求めよ。
（２）1050の約数のうち、1と1050を除く正の約数の和Sを求めよ。
（３）Sの正の約数の個数を求めよ。
（４）Sの約数のうち、1とSを除く正の約数の和を求めよ。

解答・解説

（１）1050を因数分解すると、1050=2×3×5²×7
約数は、1個の2, 1個の3, 2個の5, 1個の7の全ての組み合わせから作る。

指数の組み合わせ表から考えると以下の通り。

0	0	0	0				1	0	0	0
0	0	0	1				1	0	0	1
0	0	1	0				1	0	1	0
0	0	1	1				1	0	1	1
0	0	2	0				1	0	2	0
0	0	2	1				1	0	2	1
0	1	0	0				1	1	0	0
0	1	0	1				1	1	0	1
0	1	1	0				1	1	1	0
0	1	1	1				1	1	1	1
0	1	2	0				1	1	2	0
0	1	2	1				1	1	2	1

要するにn=2×2×3×2=24通り

これを一般化すると、

2以上の正の整数Nは、素数p1, p2, p3, …と正の整数k1, k2, k3, …を用いて、N=p1k1p2k2p3k3…の形に表すとき、 Nの正の約数の個数は、(k1+1)(k2+1)(k3+1)…である。

（２）この問題は、24個の約数を全部計算して、単純に足し算すれば求められるが、時間がかかる。
公式を知っているかどうかが大事。


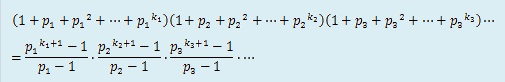
1050=2×3×5²×7だから、1050の正の約数の総和は、公式より、
　
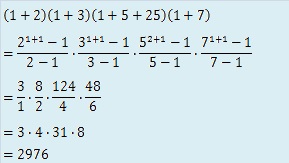
題意より、S=2976-1-1050=1925

（３）1925を因数分解すると、1925=5²×7×11
よって約数の個数は、(2+1)(1+1)(1+1)=12個

（４）1925の正の約数の総和は、公式より、
 
題意より、2976-1-1925=1050

問題４

正の整数 n の正の約数の個数を d(n) で表す。d(5)=2, d(6)=4 である。
d(n) が奇数であるとき、n は平方数（自然数の2乗の形の数）であることを証明せよ。

解答・解説

問題５

正の整数 n に対し n の正の約数すべての和を S(n) とおく。但し、1 と n も約数とする。
（１）素数 p, 正の整数 a に対し、n=p^a とおく。S(n) を p と a で表せ。
（２）相異なる素数 p, q, 正の整数 a, b に対し、n=p^a, m=q^b とおく。このとき、S(mn)=S(n)S(m)が成立することを証明せよ。
（３）正の整数 a について 2^a-1 が素数とする。このとき、n=2^a-1(2^a-1) とおくと、S(n)=2n が成立することを証明せよ。

解答・解説

→topに戻る　→代数topに戻る  →目次に戻る

開始：2013年7月11日
更新：2013年7月31日
最終：2014年3月12日
最終更新：2014年3月13日